我国省域中等职业教育综合发展水平差异比较、均衡水平与协调性分析

作者简介

李德显（1966- ），男，辽宁师范大学教育学部教授，博士生导师，教育学博士，研究方向：教育社会学，教育基本理论（大连，116029）；史晓谭（1999- ），男，辽宁师范大学教育学部博士研究生，研究方向：教育社会学，道德教育

基金项目

2022年度教育部人文社会科学研究规划基金项目“我国普通高中教育发展指数构建及区域差异研究”（22YJA880040），主持人：孟丽菊；2024年度辽宁省教育厅高校基本科研一般项目“辽宁省职业教育高质量发展指数构建及优化策略研究”（20240068），主持人：李德显

摘 要 中等职业教育高质量发展是推动我国建立现代职业教育体系的重要基础。以2021年我国31个省（区、市）教育宏观统计数据为基础，构建由入学机会、发展规模、教育质量、经费投入、办学条件5个一级指标构成的中等职业教育综合发展水平评价指标体系，采用PLS结构方程模型的方法对我国中职教育综合发展水平进行测评。研究结论如下：我国中等职业教育综合发展水平存在着贡献率差异与相关性差异的内部结构不均衡性；我国中等职业教育综合发展水平省域间差异较大，综合水平普遍不高，“金字塔”式结构特征明显；除北京、天津和吉林外，我国各省市中等职业教育均具有非均衡发展特征，且我国省域中等职业教育发展内外协调性较差。为提高我国中等职业教育发展水平，可以采取以下策略：因地制宜控制中等职业教育发展规模，加强教育质量内涵建设；非均衡发展省份补齐自身短板，促进中等职业教育优质协调发展；完善中等职业教育投入支撑体制，为中职教育发展提供坚实保障。

关键词 中等职业教育；综合发展水平；指标体系；均衡水平；协调程度

中图分类号 G718.3 文献标识码 A 文章编号 1008-3219（2024）21-0058-10

近年来，随着完善国民教育体系步伐的持续推进以及经济社会转型对高技术技能人才需求的不断加大，国家对职业教育的重视程度逐步加深。2022年5月1日，新修订的《中华人民共和国职业教育法》正式施行，明确提出职业教育是与普通教育具有同等重要地位的教育类型，是培养多样化人才、传承技术技能、促进就业创业的重要途径。中等职业教育作为构建中国特色职业教育体系的重要组成部分，主要面向初高中毕业生开展基础性的知识、技术和技能教育，为社会输送初、中级技术人员及技术工人，在促进教育公平、稳定社会发展、阻断代际贫困等方面发挥重要作用。目前，我国中等职业教育主要由普通中专、成人中专、职业高中与技工学校实施，2021年，全国共设置中等职业学校7294所（不含技工学校），招生488.99万人，在校生1311.81万人，分别占高中阶段教育招生总数和在校生总数的35.08%、33.49%[1]，中等职业教育已成为我国普及高中阶段教育、提高劳动人口素质与构建“技能型社会”的重要基础。深入研究我国中职教育的整体发展状况以及省域间的差异特征、均衡协调程度，有利于国家和各省份相关部门全面了解当前中职教育的发展状况，准确定位各地区中职教育发展的优劣势，对于提高决策的针对性、科学性与合理性，优化高中阶段教育结构，促进各省份中等职业教育协调发展，进而推动我国现代职业教育体系建设与高质量发展具有重要意义。

一、指标体系的构建与模型的建立

（一）指标体系的构建

中等职业教育作为我国在高中阶段实施的区别于普通教育的一种重要教育类型，兼具中等性与职业性的双重属性，对其综合发展水平的评价必须充分考虑其发展特殊性，进而将多种教育指标加以系统整合，方能较为准确客观地反映中等职业教育发展状况。

目前，国内已有学者对中等职业教育综合发展水平进行评价指标体系或发展指数的构建。陈嵩[2]从政府宏观调控、资源现状、服务水平三个方面进行综合评价，具体包括结构协调、发展规模、拥有资源、财政投入和资源质量5个指标。朱德全[3]构建了由入学机会、基础条件、核心发展、保障支撑和培养成效5个一级指标构成的职业教育均衡测度指标体系，并采用因子分析法和层次分析法分别对一级指标进行分解和确定各指标的权重与系数。安蓉等人[4]从教育的结构、投入、条件与质量4个方面构建了中等职业教育综合发展评价指标体系。林克松[5]则从结构协调、经费收支、教学条件、师资力量、培养成效5个二级指标共12个三级指标进行构建，同时借鉴“人类发展指数（HDI）”“全球竞争力指数（GCI）”等知名指数指标赋权及国内经验的做法，对所有指标采用等权法进行线性分配，但该指标体系忽略了办学规模以及生均图书量等重要指标。杨丽雪等人[6]补充了这一缺憾，采用熵权法建构了由办学规模、师资力量、教学条件、经费投入与培养成效5个维度构成的中等职业教育发展水平指标体系，但该体系同时又忽略了教育机会、普职结构等对评价区域中职教育发展水平极具特殊与重要意义的指标内容。

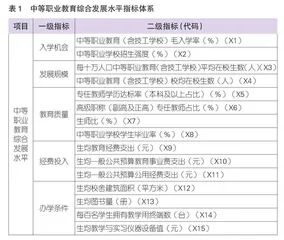
综合来看，国内学界大多注重采用具有综合性的教育发展指标或发展指数来对地区中等职业教育发展水平进行测度与比较，并且在维度或具体指标的涉及内容上已初步形成共识，出于研究目的或方法等因素使得各学者间的指标体系构建方式略有差异。本研究遵循指标体系设计科学性、系统性、代表性、可行性的原则，借鉴已有的指标体系，结合我国中等职业教育发展的实际状况，构建了一个由入学机会、发展规模、教育质量、经费投入、办学条件5个一级指标和15个二级指标组成的指标体系，见表1。需要说明的是，中等职业学校招生强度指的是以满足高中阶段教育招生的适龄人口（15～17岁）为基数的中职招生比例，内涵包括学历教育与非学历教育两个部分，能够较大程度反映区域中职教育发展的入学机会指数。此外，本研究在最初构建指标体系时设有普职结构指标，然而实际在对其进行模型检验时，发现该指标在综合水平潜变量载重负荷值及显著性方面均未达到要求，即表明普职结构在本研究中不能成为测评中职教育综合发展水平的子维度（可以理解为出于本研究方法的特殊性，默认普职结构反映的是高中阶段教育结构的协调程度而非评价中职教育内部的质量水平问题），故在最终指标体系呈现上将其剔除。

（二）研究数据、方法与工具选择

本研究所采用的数据均来自官方正式发布。其中，教育事业发展数据主要来自《中国教育统计年鉴2021》《中国统计年鉴2022》，技工学校数据来自《中国劳动统计年鉴2021》，经费数据来自《2021年全国教育经费执行情况统计表》，人口数据则来自《中国人口普查年鉴2020》。由于本研究采用除港澳台外的我国其他31个省（区、市）的截面数据进行横向比较，样本量较小，不符合协方差结构模型（CSM）样本量最少不低于200个的要求。因此，本研究选择对样本数目要求较低（30—100）且对数据分布形态无特殊要求的偏最小二乘法（partial least squares，PLS）作为研究方法。另外，由于PLS方法可以有效地克服观测变量间的共线性问题，能够去除对回归无益噪声的影响，可以使模型具有更好的鲁棒性[7]。并且该方法采用一系列一元或多元线性回归的迭代求解[8]，能够同时处理反映型指标和形成型指标结构，其在小样本数据的综合评价研究中具有良好的应用效果[9]。据此，本研究采用软件SPSS27.0和Smart PLS4.0对数据进行处理与分析。

（三）PLS结构方程模型的建立

基于上述所构建的指标体系，选择使用SPSS27.0软件对5个一级指标的二级指标分别进行单一维度检验。检验结果显示，各维度的第一主成分特征值均大于1，第二主成分特征值均小于1，也就是说各维度均通过了该项检验。使用Smart PLS4.0软件，采用PLS算法和反映型测量模型，建立我国中等职业教育综合发展水平PLS结构方程模型，见图1。模型中除了评价项“综合水平”这一潜变量外，其余5个潜变量分别代表5个一级指标。15个二级指标用x1-x15表示。这里需要说明的是，在运行模型之前所输入的数据是来源于现实的实际数据，但在采用PLS算法时，软件默认将原始数据先进行标准化，所以软件所输出的结果均为标准化结果。如无特别说明，以下均采用标准化结果进行分析。

由图1可以得到入学机会等5个潜变量对综合水平潜变量的标准化路径系数。其中对中等职业教育综合发展水平贡献最大的是办学条件，标准化路径系数为0.373。经费投入与教育质量潜变量贡献率排名第二、三位，路径系数分别为0.287和0.178。入学机会潜变量对综合水平的贡献排在第四位，其标准化路径系数为-0.160，这里的负号代表入学机会与综合水平之间呈负相关关系，而值0.160代表入学机会对综合水平贡献的大小。发展规模潜变量对综合水平的贡献最小为-0.138，排在第五位，同样与综合水平之间呈负相关。然而实际上模型得出的入学机会与发展规模两个潜变量对综合水平呈现出的负相关关系与研究最初假设正好相反。这在一定程度上可以解释为入学机会越少，出于主客观因素选择中等职业教育进行学习的个体数量就越少；而发展规模越小，意味着中职教育在校生数就越少，这都会使得现存的中职学生人均资源占有量越高，进而越有利于提高教师教学质量以及学生培养质量，也就越有利于中职教育综合发展水平的提高。此外，综合水平对入学机会等5个潜变量的多元回归方程测度系数的平方值为1.000，说明综合水平对这5个潜变量概括程度相当高，这5个潜变量对综合水平潜变量的解释力足够强。

（四）PLS结构方程模型的检验

1.拟合指标与信效度检验

从表2综合水平的R2值来看，模型中的各潜变量对综合水平的解释能力强，解释比例达到100%。此外，PLS结构方程模型的信度指标主要有合成信度CR和rho_A，要求其值均＞0.7，由表2可知各潜变量值均满足此要求，说明模型具有良好的信度。同时，评价模型效度主要是通过平均抽取变异量（AVE）来反映其聚合效度，要求其值＞0.5，各潜变量值均达到该适配标准。以上数据表明，模型整体拟合效果好，内部关系的解释功效较强，估计效果可以接受，信度佳。

2.Bootstrapping检验

利用Bootstrapping方法计算各路径系数的T统计量，检验路径系数估计的显著性水平（双尾检验）。如果2.58＞T＞1.96，则路径系数估计在0.05水平上显著。如果3.29＞T＞2.58，则路径系数估计在0.01水平上显著。如果T大于3.29，则路径系数在0.001水平上显著。表3给出了Bootstrapping检验中结构方程模型的T统计量，数据显示全部路径系数均具有较高的T统计量，说明各路径系数通过了相应显著性水平的检验。这也进一步说明了经过5000次样本重复抽样，模型结构的稳定性非常好。

3.模型外部权重及与其潜变量的相关系数

表4给出了各显变量指标与相应潜变量的相关程度，一般情况下，指标与潜变量之间相关程度越高，说明潜变量越能更好地概括指标所包含的信息。由表4潜变量综合水平及其指标可见，除X4（中等职业教育校均在校生数）、X5（专任教师学历达标率）、X6（高级职称专任教师占比）、X8（中等职业学校学生毕业率）四个指标相关系数在0.5左右外，其余11个指标的相关系数均高于0.7，说明模型较好地综合反映了观测指标的基本信息。

二、省域间中等职业教育综合发展水平的比较分析

（一）省域间中等职业教育各指标发展水平的差异比较

基于PLS结构方程模型运算后的输出数据，即各潜变量的得分情况，对我国31个省（区、市）中等职业教育综合发展水平进行比较与分析。其中入学机会与发展规模两个潜变量与综合水平之间呈负相关关系，按照Tenenhaus[10]的建议，可以将单独负相关指标的符号改变，由此得到各省份中等职业教育发展的综合水平得分和排名情况，见表5。

从中等职业教育发展的综合水平排名来看，北京、上海和西藏分别排名全国前三位，得分都在1.000以上，说明这三个地区中等职业教育综合发展水平处于全国领先地位。天津、吉林、内蒙古、辽宁、黑龙江、浙江和江苏7个省的得分在0.833～0.284之间，排名分列第4至第10位，中等职业教育的综合发展水平相对靠前，处于全国排名的前十位。而山西、宁夏、湖北、甘肃、山东、广东、新疆、福建、陕西、湖南、河北和云南得分在0.047～-0.574之间，排名分列全国第11至第22位，处于全国中游水平。贵州、安徽、江西、重庆、四川、河南、青海、海南、广西得分在-0.604～-1.180之间，排名位于全国后9位，处于全国下游水平。从中等职业教育5个单一维度的发展水平来看，在入学机会维度上排名全国前6位的分别是北京、天津、上海、吉林、黑龙江和西藏，其得分均在1.000以上，处于领先地位。因为入学机会与综合水平之间呈负相关关系，这表明该6个地区入学机会指标值要比其他省份小，即中等职业教育毛入学率和中等职业学校招生强度最低。在发展规模维度上，北京、上海、吉林、内蒙古、辽宁、天津和黑龙江排名全国前7位，得分均在1.000以上，处于明显领先地位。同样，发展规模与综合水平之间也呈负相关关系，说明这7个省份发展规模指标值比全国其他省份值小，即每十万人口中等职业教育平均在校生数和中等职业教育校均在校生数最少。在教育质量维度上，北京、吉林、江苏、天津、辽宁和上海排名全国前6位，得分均在1.000以上，处于明显领先地位。在经费投入维度上，北京、上海、西藏排在全国前3位，得分在1.000以上，处于明显领先地位。在办学条件维度上，北京和上海以得分4.440和2.226高居全国排名前两位，同样处于全国领先地位。