基于DEA-Tobit模型的“双高计划”建设高职院校办学效率评估及建设策略

摘 要 运用DEA模型评估首轮“双高计划”建设结束后56所“双高”院校的办学效率，结合截断数值Tobit回归分析，探索影响“双高”院校办学效率的影响因素。研究结果显示，“双高”院校整体办学效率较初期有所提升；“双高”院校要素投入与配置效率仍有待进一步改善；社会服务成为影响“双高”院校办学绩效的最大因素。为推动“双高计划”顺利实施，要提高要素投入与配置效率，加快“双高计划”建设绩效产出；要加强内部治理现代化改革，确保“双高计划”建设高质量推进；要瞄准社会服务水平提升，强化“双高计划”建设支撑发展作用；要优化人力资源投入与产出关系，综合提升办学效率。

关键词 “双高计划”；办学效率；高职院校

中图分类号 G718.5 文献标识码 A 文章编号 1008-3219（2024）27-0058-08

一、问题提出

2019年12月，教育部、财政部发布《关于公布中国特色高水平高职学校和专业建设计划建设单位名单的通知》[1]，其中包含高水平学校56所，高水平专业群建设单位141所，合计197所“双高计划”建设院校（以下简称“双高”院校）[2]。通过五年（2019-2023年）建设，首轮“双高计划”已经结束，本研究正是在首轮“双高计划”终期绩效评价的背景下，使用DEA-Tobit模型对56所“双高”院校办学效率进行分析，比较研究“双高”院校建设初期与终期的办学绩效，分析“双高”院校投入产出情况，评估“双高”院校在提升职业教育质量方面的发展，为下一轮“双高计划”建设过程中各高职院校提升办学效率提供参考与借鉴。

二、研究设计

（一）研究模型

传统经济学方法在测量具有投入大、产出高特点的办学活动时是十分困难的，而借用DEA数据包络法（Data Envelopment Analysis）来评估学校的相对办学效率却取得了较好的效果。DEA分析要求决策单元（分析对象）具有相同的目标、性质和外部环境，即同质性要求。这与高职院校之间具有类似办学目标、定位、办学环境等相接近，可以认为高职院校满足DEA分析对于决策单元的同质性要求。本研究先用DEA评估56所“双高”院校办学效率，再用截断数值Tobit分析办学效率的影响因素，即采用了一种DEA-Tobit两步测算法[3]来完成办学效率评估分析。

（二）数据来源

根据“双高计划”建设院校名单，选取了56所“双高”院校作为分析样本。投入与产出指标数据主要来自两方面：一是高等职业教育质量年度报告；二是教育部网站上公布的相关比赛、遴选、评比结果文件，如全国职业院校技能大赛教学能力比赛获奖名单、全国教材建设奖评比结果等。

（三）指标构建

1.指标初选

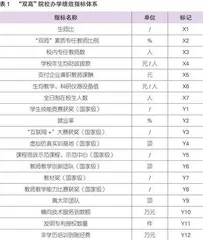
初始指标选取时参考了现有文献中所采用的指标及遴选方法。主要初选指标以马欣悦、汤霓等[4]研究成果为参考，同时还加入了部分在“双高计划”中期绩效评价中被确认为标志性成果的指标。在遵循通用性、易取性、代表性的指标筛选原则下，最终确定了初始指标体系，见表1。

DEA分析从数学原理上并不要求数据进行无量纲化处理，但在进行DEA分析时应该使用正向化指标。如果数据有负向（逆向）指标，则需要对其进行处理，让其指标意义变为正向。本研究中，生师比（生师比＝折合在校生数/教师总数）数值越大代表学校在人力方面的投入越少，因此可以理解为是一个负向指标。在SPSS 22.0中，一般采用原始变量的负数或者倒数来对其进行正向化，本文采用后者对生师比数据进行正向化处理。

在以往的研究中，例如学生技能竞赛获奖指标的单位是“项”，但是由于比赛区分一等奖、二等奖和三等奖，因此只用简单求和后的数值来表征一个学校的学生竞赛情况会造成分析结果的不准确。本文采用熵值法对上述指标进行了权重计算，并用无量纲综合得分来表征相应指标的大小，所以在本研究中，学生技能竞赛获奖（国家级）、“互联网+”大赛获奖（国家级）、课程思政示范课程、示范中心（国家级）、首届教材奖（国家级）、教师教学能力比赛获奖（国家级）共5个产出指标是无量纲的。相比以往同类研究，研究结果更具有合理性和准确性。

2.指标确定

利用DEA评估“双高”院校办学效率时，投入指标与产出指标应存在一定的相关性。将投入指标与产出指标之间进行相关性分析，可以看出，Y4、Y5、Y6、Y9与X1、X2、X3、X4、X5、X6、X7、X8共8项之间均没有呈现出显著性（p值均大于0.01），意味着Y4、Y5、Y6、Y9与X1、X2、X3、X4、X5、X6、X7、X8共8项之间均没有相关关系。因此，剔除Y4、Y5、Y6、Y9共四个产出指标。

投入指标之间相关性和产出指标之间的相关性影响着DEA分析结果，因此在DEA分析中考虑指标间相关性十分必要。智冬晓指出，用因子分析法对指标进行处理后再进行DEA分析，所得结果更符合实际[5]。王宁等指出，采用因子分析对指标进行降维处理，降低指标之间的相关性，可以提高评估结果的有效性[6]。因此，本研究利用因子分析法分别对投入指标和产出指标进行前期处理。

因子分析（探索性因子分析）用于探索分析项（定量数据）应该分成几个因子（变量），通常有三个步骤：第一步是判断是否适合进行因子分析；第二步是因子与题项对应关系判断；第三步是因子命名。本研究首先通过SPSS 22.0对7个投入指标进行因子分析，分析前先对投入指标进行KMO和Bartlett球形度检验，检验结果见表2。由检验结果可知，KMO值为0.644，大于0.5；Bartlett球形度检验p小于0.01，说明投入指标适合进行因子分析。

对投入指标进行因子分析，旋转后投入指标因子载荷系数见表3。所有指标共同度（公因子方差）均大于0.4，因此无须剔除。分别提取3个投入因素（累积方差贡献率＝83.832％）FI1、FI2、FI3。根据分析结果，将FI1命名为资金设备投入，将FI2命名为人力资源投入，将FI3命名为人才结构投入。

采用同样方法对8个产出指标进行因子分析。产出指标KMO和Bartlett球形度检验结果见表4。由检验结果可知，产出指标的KMO值为0.611，大于0.5；Bartlett球形度检验p小于0.01，说明产出指标同样适合进行因子分析。

表4 产出指标KMO和Bartlett检验结果

检验方法 值

KMO检验 0.611

Bartlett球形度检验 近似卡方 63.218

df 28

p值 0.000

对产出指标进行因子分析，旋转后产出指标因子载荷系数见表5。所有指标共同度（公因子方差）均大于0.4，因此无须剔除。分别提取了3个产出因素（累积方差贡献率＝61.105％）FO1、FO2、FO3。根据分析的结果，将FO1命名为社会服务成果，将FO2命名为师生竞赛成果，将FO3命名为教学育人成果。

根据DEA使用方法，决策单元个数（“双高”院校数量）应至少是投入与产出指标数之和的两倍以上，过多的指标数将导致分析结果不准确。本研究中，通过因子分析对指标进行降维处理后，新的投入、产出指标合计为6个。决策单元总数为56个，新的投入、产出指标数之和不足决策单元数量的一半，因此满足DEA分析要求。

因子分析后需要求出新的投入、产出因子得分，但是由于原始指标数据的单位、数量级各不相同，无法直接相加。为解决上述问题，需要进一步对原始指标数据进行标准化处理，因此本研究对原始数据采用了Z-Score标准化处理。标准化处理后，求出新的投入、产出指标因子得分。

不论是投入因子数据还是产出因子数据，只要研究数据中出现负数或者0，此时进行DEA分析并不适合。因此，采用阈值法[7]对投入、产出因子得分进行无量纲化处理，见表6。

三、实证分析

DEA数据包络分析有很多模型，其中BCC和CCR最为经典。如果考虑规模报酬可变则使用BCC模型，反之如果认为规模报酬不变则应使用CCR模型。本研究使用BCC模型进行分析。

（一）办学效率评估分析

经过指标开发与模型验证，采用SPSSAU数据科学分析平台评估56所“双高”院校的办学效率，见表7。

一般来说，综合效率值等于1时意味着DEA有效，反之综合效率值小于1意味着DEA无效。结合θ（综合效率）、S-（投入冗余）和S+（产出不足）数值，可判断DEA有效性，其中S-和S+数值在表7中未给出。办学效率有效性统计结果见表8。

根据效率划分标准，当θ≥0.8时，表面研究对象办学效率较高；当0.5≤θ＜0.8时，表面研究对象办学效率中等；当θ＜0.5时，表面研究对象办学效率较低[8]。整理56所“双高”院校的综合办学效率，其办学效率分布情况见表9。

根据可变规模报酬下的BCC模型分析结果可以得到资源配置的纯技术效率，表示在同一规模的最大产出下最小的要素投入成本[9]，可以衡量投入导向下的各“双高”院校的技术无效有多少是由纯技术无效而导致的。依据纯技术效率和规模效率是否达到全国平均水平，将全国56个“双高”院校分为四类[10]：一是纯技术效率和规模效率大于全国平均值，说明这部分院校教育资源配置是相对有效的；二是纯技术效率高于全国平均值而规模效率小于平均值，说明这部分院校由于规模效率低下，进而导致综合效率的相对无效；三是纯技术效率和规模效率均小于全国平均值，表明这类院校综合效率相对低下，这主要源于两类效率均较低；四是纯技术效率小于全国平均值而规模效率大于平均值，说明这部分院校的纯技术效率有待进一步提高。经过整理，全国56所“双高”院校配置效率的分类结果见表10。

（二）投入产出问题分析

通过DEA模型评估发现，中等及以下办学效率的院校有29所，占比51.79%。规模效率等于1的院校只有11所，占比19.64%。规模效率能够很好地反映出决策单元的投入产出问题，规模效率不等于1，则说明需要调整研究对象的规模[11]。通过规模效率检验发现，规模递增的院校有27所，说明这些规模递增院校的成果产出增长比例比成本投入增长比例高，适合进一步增加投入。规模递减的院校有18所，说明这些规模递减院校的成果产出增长比例比成本投入增长比例低，并不适合进一步增加投入。见表11。

运用松弛变量进一步考究“双高”院校的投入产出问题。在投入方面，FI1投入冗余的院校有7所，其中以学校编号为24（松弛变量S-值高达2.424）的学校为代表，这类学校在资金投入上相对较高。FI2投入冗余的院校有12所，其中以学校编号为7（松弛变量S-值高达1.159）的学校为代表，这类学校在人力资源投入上相对较高。FI3投入冗余的院校有4所，其中以学校编号为32（松弛变量S-值高达1.857）的学校为代表。值得注意的是，没有一所学校同时具有2个或全部指标投入冗余的情况。见表12。

在产出方面，FO1产出不足的学校有8所，其中以学校编号31（松弛变量S+分析值高达3.457）为代表。FO2产出不足的学校有12所，其中以学校编号3（松弛变量S+分析值高达6.659）为代表。FO3产出不足的学校有21所，其中以学校编号7（松弛变量S+分析值高达3.667）为代表。同时有两项指标产出不足的学校有5所，占比8.93%，学校编号分别是3、8、7、17、43，相对而言此类学校存在较严重的产出不足问题。没有一所学校同时有三项指标产出不足，这也说明全国56所“双高”院校至少在某一方面取得较为可观的成果。见表13。

因此，从各学校投入产出问题分析可以看出，在非DEA有效的“双高”院校中产出不足问题相较投入冗余问题更加复杂。从投入产出的结构去提高高职院校尤其是非DEA有效的院校办学效率仍然需要不断地研究与探索。

（三）效率影响因素分析