职业院校课堂生态量表的编制与应用

摘 要 职业教育的高质量发展必须根植于课堂中，用生态哲学观观照新时期的课堂教学实践是深化课堂研究的新视角和新方法论。这一新的转向需要加强职业院校课堂生态研究，而编制适用于职业院校课堂生态量表这一基础性工具就成为关键而重要的工作。通过量表的编制、预测、修改和再测，最终确定了包括合作与秩序、教师参与、教师支持、课堂环境、学生参与、关系6个维度和32个题目的职业院校课堂生态量表，该量表的内在一致性信度为0.968，分半信度为0.849，验证性因素分析结果表明该量表具有较高的效度。运用该问卷对江苏省5所职业院校的学生进行问卷调查，分析课堂生态情况，实践证明该量表适合于研究职业院校课堂生态，能为职业教育实践者评价职业院校课堂教学效果提供一个经济、简单和有效的测量工具。

关键词 职业院校；课堂生态；量表编制；课堂教学

中图分类号 G712 文献标识码 A 文章编号 1008-3219（2023）08-0023-08

一、引言

教育部等九部门印发的《职业教育提质培优行动计划（2020—2023年）》提出：“加强课堂教学日常管理，规范教学秩序。推动职业学校‘课堂革命’，适应生源多样化特点，将课程教学改革推向纵深。”[1] 当前职业院校课堂中的诸如教师倦怠教态、学生无助学态以及课堂沉闷状态等生态性问题，制约甚至阻碍着职业教育质量的提高和内涵建设。因此，建设生态课堂是未来课堂改革的方向[2]，有必要加强对职业院校课堂生态的研究。

近年来课堂生态研究主要集中在：新课程和教学方法对课堂生态的影响；课堂生态的影响因素；课堂生态与学业成就的关系；课堂生态测量工具的发展等。其中，尤以课堂生态测量工具的发展和课堂生态与学生学习成果方面的研究较为引人注目[3]。国外研究者已经开发出多种课堂生态量表，主要有学习环境量表（LEI）、我的课堂量表（MCI）、科学实验室环境量表（SLEI）、建构主义课堂环境量表（CLES）、课堂环境量表（WIHIC）等[4][5]。然而在职业教育领域，目前国内外关于其课堂生态的量化研究均存在不足，集中表现在缺少较为科学的课堂生态测量工具。因此，有必要根据现阶段职业院校课堂的实际情况，编制出适合职业教育的课堂生态量表。本文主要参照Moos的三层面结构理论，基于“香港课堂环境量表（HCES）”中文版“课堂生态量表”[6][7]，以文献研究和已有相关问卷、量表为基础，编制适合于职业院校的课堂生态量表，为职业教育实践者评价职业教育课堂教学效果提供一套经济、简单和有效的测量工具。同时对该量表的适应性进行分析，对职业院校课堂生态的现状与问题进行剖析，认清问题并找出问题的症结所在，探索有效解决相关问题的对策。

二、研究方法

（一）编定初始量表

考虑到职业院校课堂的延展性和课堂主体的复杂性，对中文版“课堂生态量表”的维度和题项进行增删和调整，经课题组共同研讨，形成初始问卷。初始问卷分为现实课堂生态和理想课堂生态两个部分，由55个初试项目组成，其中包括10个反向计分题。“合作”维度具有5个项目，“秩序”维度具有5个项目，“学生参与”维度具有5个项目，“关系”维度具有10个项目，“教师参与”维度具有10个项目，“教师支持”维度具有10个项目，“课堂环境”维度具有10个项目。问卷采用李克特5点计分法，其中，1=从不如此、2=偶尔如此、3=有时如此、4=经常如此、5=总是如此。

（二）预备测试

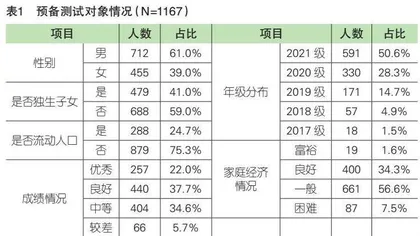
选择在江苏省5所中等职业学校发放问卷。通过网上问卷星的方式，将问卷链接发在各个班级群里，由班主任督促学生完成问卷。共回收问卷1500份，根据作答时间（删除作答时间太短或太长的问卷）以及作答内容（删除连续10个或10个以上的答案选项是相同的问卷）删除无效问卷，得到有效问卷1167份，问卷有效率为77.8%。有效样本中，被试年龄范围为14～23岁，平均年龄为16.54岁（SD=1.071）。预备测试对象情况详见表1。

（三）正式施测

为了确定量表结构的合理性以及对量表的信度和效度进行检验，我们进行了正式测试。正式样本来自江苏省某中等专业学校的学生。回收问卷376份，有效问卷364份，有效率96.8%。量表的施测过程与预测相同。有效样本中，被试年龄范围为14～20岁，平均年龄为16.60岁（SD=1.000）。正式施测对象情况详见表2。

（四）数据统计

采用SPSS 21.0进行统计分析。首先采用SPSS转换问卷项目的反向计分，再运用独立样本t检验、相关分析、信度检验分析、探索性因子分析对问卷数据进行整理与分析。验证性因子分析采用的计算工具是AMOS 24.0。

三、结果分析

（一）项目分析

项目分析的主要目的在于检验编制的问卷中个别题项的适切性和可靠程度，项目分析的检验就是探究高低分的被试在每个题项的差异或进行题项间同质性检验，项目分析的结果可作为个别题项筛选或修改的依据。依据吴明隆的观点进行项目分析[8]，方法和步骤如下：本问卷通过t检验显示，其中第25题的高低分组上的差异p值大于0.05，应予以删除，其余题项p值均小于0.05。本问卷通过题总相关分析显示，第7题、第9题、第17题、第19题、第25题、第43题的分值与总分的相关均小于0.4，应予以删除。

共同性表示项目能解释共同特质或属性的变异量，如将职业院校课堂生态量表限定为一个因素时，表示只有一个心理特质，因而共同性的数量愈多，表示能测量到此心理特质的程度愈高；相反，如果项目的共同性低，表示此项目能测量的心理特质的程度低，共同性低的项目与问卷的同质性小，应考虑删除。至于因素负荷量则表示项目与因素（心理特质）关系的程度，项目在共同因素的因素负荷量愈高，表示项目与共同因素的因素负荷量愈低，表示项目与共同因素（总问卷）的关系愈不密切，亦即其同质性愈低。一般而言，共同性值若低于0.20（此时因素负荷量小于0.45），表示项目与共同因素间的关系不密切，此时该项目可考虑删除。第7题、第9题、第10题、第16题、第17题、第18题、第19题、第20题、第25题、第43题的因素负荷量分别为0.003、0.256、0.316、0.331、0.278、0.360、0.270、0.352、-0.093、0.200，这10个项目与共同因素“课堂生态”的程度关系微弱，依此标准可考虑将此10个项目删除。

信度检验旨在检验项目删除后，整体问卷信度系数的变化情形。如果项目删除后的问卷信度系数比原先的信度系数高出许多，则此项目与其余项目所要测量的属性或心理特质可能不相同，代表此项目与其他项目的同质性不高，在项目分析时可考虑将此项目删除。本问卷整体内部一致性α系数为0.973，其中，第7题、第9题、第19题、第25题、第43题的题项删除后的α值分别为0.974、0.974、0.974、0.975、0.974，高于整体值，应予以删除，其余项目均小于或等于0.973。

综上，通过项目分析，删除初始问卷项目的第7题、第9题、第10题、第16题、第17题、第18题、第19题、第20题、第25题、第43题共10个项目后，初试问卷还剩45个项目。

（二）因素分析

1.探索性因素分析

通过探索性因子分析来检验初始量表的结构效度。本初试问卷的KMO值为0.975，表示变量间具有共同因素存在，变量适合进行因素分析。此外，Bartlett球形检验的卡方值为38610.988（自由度为496，p<0.001），表明数据非常适合进行因素分析。

为对初试问卷中各项目进行筛选并形成职业院校课堂生态量表正式问卷，用主成分分析法提取特征值大于1的因子，方差极大正交旋转确定因子负荷，保留负荷大于0.5的项目。为了使问卷更加的简洁有效，需要对此问卷项目进行删减。结合以往研究和本研究对课堂生态结构的假设，对此进行多次探索性因素分析，并按以下几个标准删除初试问卷中不合适的题项：一是共同度小于0.3。项目的共同度反映了公因素对该项目的贡献，共同性越高，表示能被公因素解释的程度越高，说明该题目的作用越大。二是项目负荷量小于0.5。项目的负荷量说明公因素与该题目的相关程度，题目的负荷量越小，说明该题目与公因素之间的关系不大，表示该题目不能够将公因素所代表的心理特征反映出来。三是每个因素包含的题目不得少于3个。经过多次探索，删除第8题、第24题、第26题、第32题、第33题、第36题、第37题、第42题、第45题、第46题、第52题、第53题和第54题13个项目后，最终获得6个因子，可以累积解释变异量为78.347%，因子负荷范围为0.508～0.830。对6个因子进行深入分析发现，维度结构比较清晰，根据项目内容分别命名为合作与秩序（6）、教师参与（6）、教师支持（6）、课堂环境（6）、学生参与（5）和关系（3），详见表3。此外，这6个因素旋转后的特征值分别为5.323、5.237、4.566、4.361、3.799、1.784。由此可得出，合作与秩序、教师参与、教师支持、课堂环境和学生参与对于职业院校课堂生态的影响相对较大。

2.信度分析

为进一步了解问卷的可靠性和稳定性，需对问卷做信度检验。本问卷采用内部一致性系数，即克隆巴赫α系数对问卷进行信度分析，得出该问卷的内部一致性系数为0.968，对问卷进行分半系数分析，Spearman-Brown系数为0.849，表明此问卷的信度较高，将其作为职业院校课堂生态的测量工具是可靠的。

3.效度分析

本研究通过各维度之间以及各维度与总分之间的相关分析，来检验量表的结构效度。结构效度常用的分析方法是因素分析法。根据因素分析结果，见表4，本量表各维度与量表总分的相关系数在0.818～0.853之间（p<0.05），属中高度相关，表明维度之间具有一定的独立性，并且各维度较好地反映了量表所要测量的内容。量表各维度之间的相关系数介于0.542～0.766之间（p<0.05），属中度相关，显示量表的各维度间的区别效度较为合理，各维度所评测的构念在大方向上较为一致，而各维度之间又可区别，因此，自编量表的结构基本符合编制要求，具有良好的结构效度。

4.验证性因子分析

验证性因子分析指对已有理论模型与数据拟合程度的一种验证[9][10]。通过验证性因素分析，一方面分析外因潜变量和观测变量之间的相关和负荷，从而反映各因素之间的路径；另一方面分析拟合指标反应模型的拟合程度。采用极大似然估计，对现实课堂中的合作与秩序、教师参与、教师支持、课堂环境、学生参与、关系构成的六维度结构进行验证性因素分析，测量模型见图1。其中，ACO6指现实课堂合作与秩序（包含6个项目，分别是1、2、3、4、5、6）、ATI6指现实课堂教师参与（包含6个项目，分别是27、28、29、30、31、41）、ATS6指现实课堂教师支持（包含6个项目，分别是34、35、38、39、40、44）、ACE6指现实课堂环境（包含6个项目，分别是47、48、49、50、51、55）、ASI5指现实课堂学生参与（包含5个项目，分别是11、12、13、14、15）、ARE3指现实课堂关系（包含3个项目，分别是21、22、23）。6个维度的因子负荷均可接受，6个维度间的相关系数较为合理，模型图清晰地验证了6个维度结构的合理性。

本研究对该模型的评价指数和标准如下：

χ2值受样本规模的影响较大，故而一般用χ2/df作为检验样本协方差矩阵和估计协方差矩阵间相似程度的统计量。其理论期望值为1，χ2/df越接近1，表示协方差矩阵和估计的协方差矩阵之间的相似程度越大，模型的拟合度越好。本研究中χ2/df=2.742，小于3，适配理想。

常用的拟合指数有递增拟合指数（IFI）、相对拟合指数（CFI）、标准拟合指数（NFI）、拟合优度指数（GFI）等，这些指标的值均在0～1之间，越接近1越好，表示模型的拟合度较好。由表5中得知，IFI、CFI和TFI都在0.9以上，NFI=0.889，GFI=0.818，指数在可接受范围，因此职业院校课堂生态模型的整体数据拟合较好。

近似均方根误差（RESEA）小于0.05表示模型拟合很好，而在0.05～0.08之间表示模型拟合较好，在0.08～0.10之间仍可接受，但如果大于0.10，则表明这个模型拟合不佳。本研究中RESEA=0.069，小于0.08，适配理想。