技能型社会建设背景下职业教育公共服务供给绩效评价指标体系构建

摘 要 建立健全职业教育公共服务供给质量长效评估机制既是技能型社会构建的基本前提，也是推进职业教育内涵建设、全民技能习得迭代的重要基础。通过问卷调查对初步梳理出的职业教育公共服务供给绩效评价27个因素进行调研，采用问卷调查法收回104份职业院校教师、政府公共服务机构人员的调研结果，并邀请8名相关专家对调查数据进行评价。通过信效度分析，最终构建了包含社会主观满意度、客观教育产出、财政投入与产出、院校基础设施建设、教学质量保障、教育资源公共服务普及、教师队伍建设7个一级指标的职业教育公共服务供给绩效评价指标体系。同时，提出建立质量与效率并存标准体系、加大政府与社会扶持力度、实现服务与供给数字化等建议，以期推动我国职业教育公共服务供给高质量发展，为技能型社会建设注入新活力。

关键词 技能型社会；职业教育；公共服务供给绩效；评价指标体系

中图分类号 G717 文献标识码 A 文章编号 1008-3219（2023）08-0067-06

一、引言

2021年10月，中共中央办公厅、国务院办公厅印发的《关于推动现代职业教育高质量发展的意见》明确指出，“到2035年，职业教育整体水平进入世界前列，技能型社会基本建成”。在此背景下，加速职业教育全生命周期公共服务转型与变革是推进职业教育高质量发展的重要路径[1]。职业教育公共服务是指以密切关注社会经济和产业发展需求为目的，通过技能习得与迭代服务经济民生的供给体系，强调政府统筹管理、惠及全员，其内容包括在职业教育领域实施的全部公共服务活动[2]。职业教育公共服务具备主体多元、技能多样等特征，可以满足社会全员对劳动技能和对美好生活的需求，推动学历社会向技能型社会转型，为职业院校培养高素质技术技能人才赋能[3]。2022年7月，教育部办公厅印发《国家智慧教育公共服务平台接入管理规范（试行）》，旨在进一步加大教育公共服务投入，加快推进数字化转型。这一战略部署为职业教育公共服务转型与变革提供了重要支撑，倒逼现代职业教育产教深度融合，面向全员展开全周期、全省域、全过程、全技能、高质量且公平的职业教育公共服务供给。但不可忽视的是，当前职业教育公共服务还停留在“就业导向、岗位技能驱动”的学校教育服务和在职培训服务层面，过分强调“职业技能”标签，导致相关服务质量、服务水平还不高[4]。技能型社会建设背景下，如何高效、客观、可靠、准确地评价职业教育公共服务供给绩效成为亟待解决的问题。由于目前国家尚未针对职业教育公共服务供给绩效评价给出统一评价标准与评价方法；学术界也尚未形成公认的理论体系，且关于评价指标取舍、评价维度的选择方面严谨性不足，缺乏关于评价指标体系信度和效度的探究。因此，为明确职业教育公共服务供给现状和评估成效，基于技能型社会建设开展职业教育公共服务供给绩效评价研究显得尤为重要。

二、评价指标初选

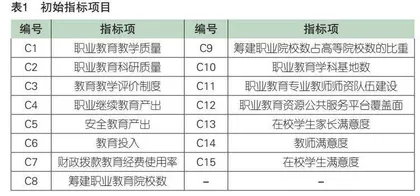
职业教育作为横跨教育与经济双领域的跨界式教育，其内涵、特征、功能及目的均需依托经济发展实现动态变化[5]。与此同时，技能型社会的提出，也预示着职业教育将朝着高质量发展方向持续前进。值得注意的是，要实现职业教育高质量发展、满足技能型社会对职业教育提出的要求，基本前提是要推动职业教育公共服务供给职能有效发挥[6]。据此，为探究技能型社会背景下职业教育公共服务供给绩效现状，本研究在充分考量技能型社会对职业教育变革发展总体要求的基础上，围绕已有研究成果，梳理并整合了评价职业教育公共服务供给绩效的27个因素。这些因素为初始指标池，一定程度上可有效反映地区经济发展水平的宏观目标，还可展现职业教育公共服务供给现状的微观目标。借助德尔菲法，邀请15名专家和高职院校教师预测指标池中27个指标及其评价结果的相关性、可信度、有效性。预测开始前，需将有关此方面的研究成果、国家相关政策、技能型社会要求、经济发展水平、职业教育发展现状、职业教育公共服务供给绩效评价价值等有关资料一并以书面形式发至所邀请专家，经由专家各自作出评估。历经三轮反馈和讨论后，各专家所给出意见均较为接近。最终，筛选和整合相关结论，挑选出与职业教育公共服务供给绩效评价最相关的15项初始指标，具体见表1。

为深入探查所选15个指标与职业教育公共服务供给绩效的关联性，特别向职业院校教师、政府公共服务机构人员下发调查问卷120份。回收有效问卷104份，有效率为87%。问卷采用李克特五分量表法，从1～5分别表示“非常不重要”“不重要”“一般”“重要”“非常重要”。同时进一步使用SPSS软件对有关调查成果展开初步分析。

三、信度与效度分析

（一）信度分析

通过数据运算发现，职业教育公共服务供给绩效评价指标体系的总体Cronbach’s α值为0.877，介于0.8～0.9区间，说明所选整体量表拥有较高可信度，且量表层面的信度同样较为理想。剔除该项指标后整体量表的Cronbach’s α值详见表2。其中，仅C13的Cronbach’s α值（0.878）较总体评价指标体系Cronbach’s α值（0.877）大，这意味着剔除C13值后，可有效提高整体评价指标体系的Cronbach’s α值，故删除该项。

进一步进行斯皮尔曼等级相关性分析后可知，C13与整体量表的相关系数为0.301。除此之外，其他项目同整体量表的相关性系数均处于0.421～0.575区间内，且相伴系数均位于0.000～0.008区间。这反映出各指标与整体量表在置信度（双侧）为0.01时，存在明显相关性与较强一致性。

（二）效度分析

效度一般分为实证效度、内容效度与结构效度[7]。其中，实证效度即效标关联效度，通常用来反映量表测度结果及其与对应外在效标间的一致程度。鉴于学术界尚未就效标提出明确参考标准，故本文暂不对量表开展实证效度评估。内容效度用于反映项目指标对所需预测内容和行为范围选取的适应程度。结构效度指测试结果可较大程度佐证理论假设。综上，采用内容效度与结构效度两种效度分析方式展开分析。

1.内容效度

除剔除C13指标外，邀请8名专家学者对职业教育公共服务供给绩效评价指标体系的内容效度进行分析，具体计算公式如下：

公式中，N为专家学者数量，Ne表示能较好测量对应于评估内容的专家学者数量。表3为运算后各指标的内容效度。

由表3可知，7名专家认为评价指标C6和C9可较好反映对应评价内容，占全部人数的87.5%；8名专家全部认为剩余12个评价指标均可较好反映对应评价内容，占比高达100%。据此可知，所选评价指标体系的内容效度符合要求。

2.结构效度

当测评量表的KMO值超过0.5，且Bartlett球形显著检验概率低于0.05时，说明评价指标体系具备构造效度，此时可运用因子分析法进行检测。因此，利用因子分析法测度量表（剔除项目C13）结构效度。经统计分析运算，所构量表的KMO值为0.713、Bartlett球度检验的近似卡方值为780.516、相伴概率Sig.值为0.000。由此可知，该量表具备良好结构效度，适用因子分析。

在KMO检验后，进一步采用主成分分析法抽取量表中特征值大于1的因子。在此基础上，选用最大方差法的旋转方法，围绕“按大小排序”和“取消小系数”两个复选框，并设置0.40为小系数绝对值。在一系列操作后，对量表进行探索性因子分析，同时旋转二十次迭代后收敛，结果见表4。

由表4可知，课题组对量表进行结构效度检验时共提取公因子7个，其中因子1有2个题项、因子2有4个题项、因子3有4个题项、因子4有1个题项、因子5有2个题项、因子6有2个题项、因子7有3个题项。进一步对7个公因子展开克隆巴赫信度检验，结果证明Cronbach’s α值整体处于0.633～0.776之间，说明各公因子信度较高。

四、指标体系构建与权重确定

（一）构建层次结构模型和AHP评价尺度

结合上述分析，首先将7个因子即一级指标设定为第一层次、14个题项即二级指标设定为第二层次，并围绕因子分析结果，建立第一层与第二层各指标题项间的对应关系。表5为依据前文所构层次指标框架。其次，采用九级比例标尺，经两两比较后构建赋值表，并以数字1～9进行标准化规范，即设定1、3、5、7、9为赋值分析尺度，2、4、6、8为介于其间的值。层次分析法每一评价尺度的内涵如下：“1”为同一维度两个评价指标均重要，“3”为其中某一个项目略微重要，“5”为其中一个题项相当重要，“7”为其中一个显著重要，“9”为量表中有一个题项绝对重要，“2、4、6、8”依次表示指标间重要性程度介于上述相邻尺度的中间，即1和3、3和5、5和7以及7和9之间。最后，设定上述9个数值的倒数，具体含义为：当指标X与指标Y进行两两比较且赋值1～9中任一数值，则指标Y与指标X进行对比时被赋值该数值倒数。

（二）构建判断矩阵

本研究累计挑选8所高职院校中15名专家根据上述评价尺度填写量表。具体而言，第一，在详细介绍各指标内涵及背景基础上，经由各专家围绕上述评价尺度及在题项两两比较后填写判断表，若涉及倒数暂不填写。第二，取判断表的平均值，并将可能涉及到的倒数值以单元格形式补齐，形成最终判断值。综上，形成第一层矩阵A和第二层判断矩阵B1～B7。以判断矩阵A为例，见表6。

（三）计算层次单排序和总排序

在上述判断矩阵基础上，进一步借助方根法计算各层次中与上一层次某指标相对应的各题项权重值。其中，第一层次只计算层次单排序；第二层次在第一层基础上再次对总排序进行计算。以判断矩阵A为例，计算过程如下：

首先，对判断矩阵A中各行乘积Mi（i=1，2，…，7）进行计算；其次，对Mi的n次方根Ri（i=1，2，…，7；n为矩阵阶数）展开计算；最后，归一化处理相应结果，得出本层中与上层某指标对应的各题项权重值。计算公式如下：

依照上述方法对判断矩阵A的层次单排序进行计算，得出各项目权重值；同理计算判断矩阵B1、B2、…、B7的层次单排序结果（权重），分别以b1、b2、…、b7来表示，具体见表7。

表7中第（4）列为二级指标C1、C2、…、C15（不包含C13），第（5）列为二级指标层次单排序结果。根据上文所述，B1的单排序结果为b1，则可设定C1、C2、…、C15（不包含C13）的单排序结果分别为c1、c2、…、c15（不包括c13）。由此可知，C1、C2、…、C15（不包含C13）的层次总排序结果分别以c1b1、c2b1、c3b1、c4b2、c5b2、c6b3、c7b3、c8b4、c9b4、c10b5、c11b5、c12b6、c14b7、c15b7进行表示。经过统计计算得出二级指标层次总排序具体数值，见表7。

（四）一致性检验

前文所述，判断矩阵是根据指标两两对比所构，能对每一阶段中各要素的相对重要性作出评估[8]。此过程中，不同判断主体对相同事件的判断可能会出现不一致结论，使得判断矩阵产生部分统计错误。具体而言，当判断矩阵阶数变大时，偏差范围也会扩大。若一致性偏离程度处于合理范围内时，判断矩阵才可被有效接受。在本研究中，仍旧采用一致性指标（C.I.）与随机一致性比率（C.R.）两个参数测度判断矩阵异质性。需注意的是，C.I.值缩小时，意味着判断矩阵偏离完全一致性的可能程度同样变小，但当阶数n在判断矩阵中的值增大时，表明人为引致偏离一致性指标C.I.的数值也变大。为解决这一问题，还需将随机一致性比率C.R.纳入，避免判断矩阵完全一致性程度扩大，从而影响整体结果的准确性。具言之，当C.R.=0时，说明判断矩阵存在完全一致性；当0<C.R.<0.1时，表示判断矩阵存在满意一致性；当C.R.>0.1时，则认为判断矩阵不存在一致性。以判断矩阵A为例，检验判断矩阵的一致性做法如下：