中等职业教育与经济增长的时序耦合及体系建构

摘 要 中等职业教育是促进区域经济增长的重要教育类型。以西部八省（自治区）为样本，基于2000-2020年中等职业教育与经济增长相关变量的时间序列数据，运用 Johansen协整检验、Granger因果关系检验等方法，分析中等职业教育与经济增长的耦合关系发现：西部地区中等职业教育与区域经济呈现单向耦合关系，中等职业学校在校生数每增加1%，人均GDP增加1.781%；中等职业学校在校生数每增加1%，城镇居民人均可支配收入增加1.395%；中等职业学校在校生数每增加1%，农村居民人均纯收入增加1.532%。高质量发展目标驱动下，西部地区中等职业教育必须深化改革，由“县”向“市”级上移中等职业学校管控权，破解“城”“乡”间的服务区隔，实现技能培训和系统教育双轴联动，构建类型鲜明、终身导向的人才培养模式，建成“空间—结构—要素”立体化、全方位的经济服务耦合体系。

关键词 中等职业教育；经济增长；区域经济；耦合性；格兰杰

中图分类号 G718.3 文献标识码 A 文章编号 1008-3219（2022）28-0031-07

一、问题的提出

西部地区职业教育是新时代职业教育现代化建设的重要部分，同时也是我国在后扶贫时代继续推进乡村振兴战略的核心抓手，各类中等职业学校以传递职业技能知识为媒介，为提升西部地区人口生产力，服务西部地区经济社会发展发挥了重要作用。

所谓“经济增长”，刘易斯（Lewis）在其著作《经济增长理论》将其定义为“按人口平均的产出的增长”[1]，即人均GDP，或“一国潜在GDP或国民产出的增加”[2]。19世纪40年代，李斯特（Friedrich List）在其代表作《政治经济学的国民体系》一文中，运用到了“精神资本”的概念，分析了教育在经济发展过程中产生的作用[3]。国内学者厉以宁在《教育经济学》中强调了智力投资的生产性问题，提出了“教育的社会经济功能”“知识与技能标准分”等概念[4]，中等职业教育的社会经济功能具体表现在其就业功能的发挥，尤其在西部经济发展相对落后的地区，中等职业教育能够为学生提供进入就业市场必要的技术技能，满足当地就业市场对中级技能人才的需求，形成合理的人才结构。罗伯特·索洛（Robert M.Solow）[5]、舒尔茨（Schultz）[6]、圣保罗（Saint-Paul）[7]、克莱门特（ClimentA）和卡布里亚娜（CabrillanaA）[8]、马金森（Marginson）、田中（Tanaka）等也充分论证了教育与经济增长存在的正相关关系。杭永宝在柯布—道格拉斯生产函数基础上，借鉴并修正丹尼森（E.F.Denison）和麦迪逊（A.Maddison）的教育对经济增长贡献测算方法，构造出教育投入的劳动增长型生产函数，计算出1993-2003年、1993-2004中等职业教育对经济增长的贡献率分别为1.910%和1.859%[9]。朱新生构建了中等职业教育发展对产业结构调整贡献的分析模型，发现中等职业教育发展对产业结构调整具有一定作用，但各地区中等职业教育发展对产业结构调整贡献的表现形式和贡献率存在差异[10]。杨梓樱运用1985-2017年数据，计算中等职业教育对经济增长的贡献率为2.595%[11]。朱德全、杨磊通过构建乡村振兴发展指数，并以柯布—道格拉斯生产函数为基础测度职业教育对乡村振兴的贡献率为16.20%[12]。还有一些学者从私人收益率的视角分析中等职业教育对区域经济的贡献。祁占勇、谢金辰通过实证研究发现，中等职业教育提高农村劳动力收入的作用强于普通高中教育，中等职业教育的相对回报率为8%[13]。综上所述，学者们从宏观与微观层面探究了中等职业教育对个人收益率或GDP指数的贡献率，遵循教育→劳动力素质提高→人力资源质量提升→经济（产业GDP或个人收入）增长的惯性思路进行研究，但鲜有学者关注西部地区中等职业教育与区域经济的互动关系。因此，本研究基于2000-2020年中等职业教育与经济增长相关变量的时间序列数据，运用Johansen协整检验、Granger因果关系检验等实证方法，研究我国西部地区中等职业教育与经济增长的耦合关系。

二、研究设计及分析

（一）研究假设

西部地区中等职业教育服务区域经济增长是一项关涉制度建设、资源共享、功能整合的系统工程，需要中等职业教育系统与区域经济系统的深度耦合，即要求两个系统通过各种相互作用而彼此影响。所谓“耦合度”是对系统之间关联程度的一种度量，描述系统或要素之间彼此相互影响、相互作用的强弱程度[14]，中等职业学校主要面向区域经济、产业及民生办学，2020年11月，教育部在《关于进一步深化职业教育东西协作，巩固脱贫攻坚成果的提案》答复中强调，“重点支持每个地市原则上至少建设好一所中等职业学校”，同时指出，“把发展中等职业教育作为普及高中阶段教育和建设中国特色现代职业教育体系的重要基础，保持高中阶段教育职普比大体相当”。对此，本文提出研究假设：

H1：西部地区经济增长是影响中等职业教育发展的原因；

H2：西部地区中等职业教育规模是影响经济发展指数的原因；

H3：西部地区中等职业教育投入对农村经济增长的回报效益大于城镇经济回报效益。

（二）指标选取与数据来源

1.指标选取

本研究旨在探究中等职业教育规模与区域经济增长的关系，教育规模的评价指标通常包含学校数量、在校生数量、生均职业教育经费投入以及专业数量等；经济发展水平评价指标一般包括GDP、人均GDP、财政收入、财政支出、农村居民家庭人均纯收入、城镇居民家庭人均可支配收入、三大产业产值及其占GDP的比重等。根据需要，本研究选取西部八省（自治区）的中等职业学校在校生数（单位：人）作为中等职业教育发展的指标；选择人均GDP（单位：元）、城镇居民家庭人均可支配收入（单位：元）、农村居民家庭人均纯收入（单位：元）作为经济发展指标。

2.数据来源

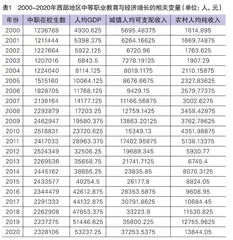
本研究以西部地区八个省（自治区）（以下简称西部地区），即广西、云南、内蒙古、贵州、新疆、宁夏、青海、西藏为研究对象，并将拟筛选的时间序列数据年份设定在2000-2020年，对《中国统计年鉴》《中国教育年鉴》以及八省区地方统计年鉴、经济统计年鉴、教育事业统计年鉴等资料进行全面搜集。具体数据见表1。

（三）西部地区中等职业教育与经济增长的相关性分析

利用SPSS25.0软件的皮尔逊积差相关法分析西部地区中等职业教育与经济增长的相关关系。分析结果见表2。

由表1可以得出，中职在校人数与人均GDP的皮尔逊相关系数为0.754，双侧显著性系数为0.000，小于0.05，呈显著性相关；与城镇人均可支配收入的皮尔逊相关系数为0.686，双侧显著性系数为0.001，小于0.05，呈显著性相关；与农村人均纯收入的皮尔逊相关系数为0.632，双侧显著性系数为0.002，小于0.05，呈显著性相关。

综上可知，西部地区中等职业学校在校生数与人均GDP、城镇人均可支配收入、农村人均纯收入均存在密切相关关系，即说明西部地区中等职业教育规模与经济增长具有相关关系。然而，相关关系仅可说明变量间存在一种不确定的数量依存关系，但具体变化的数值无法确定。因此，在验证变量相关的基础上运用格兰杰因果检验，进一步考察西部地区中等职业教育与经济增长是否具有因果关系。

（四）单位根检验

协整分析所针对的时间序列必须是非平稳的且具有单位根。因此，首先对研究的数据进行单位根检验，然后建立非平稳时间序列的回归模型。具体而言，利用Eviews11.0软件分别对变量的时间序列进行单位根检验，根据研究需要，对人均GDP、城镇人均可支配收入、农村人均纯收入、中等职业学校在校生数四组时间序列数据取自然对数，分别表示为LnTGDP、LnCZ、LnNC、LnZXRS，以此来减少数据中存在的异方差性和数据波动性，然后对这四组变量进行ADF检验，结果见表3。

由表3可知，在2000-2020年间，LNTGDP、LNCZ、LNNC、LNZXRS这4个变量的时间序列在1%、5%、10%的显著性水平上均为非平稳序列，存在单位根。经过一阶差分后，仍未通过5%的显著性水平检验，故对其二阶差分。经过二阶差分之后，4个变量的ADF检验值在5%的显著性水平上均小于临界值，因此，LNTGDP、LNCZ、LNNC、LNZXRS变量的时间序列为二阶单整，说明变量间存在协整关系，需对其进一步进行协整性检验。

（五）建立VAR模型

传统的VAR理论要求模型中每一个变量都是平稳的，对于非平稳时间序列需要经过差分至平稳序列后才可以建立VAR模型，但差分往往会导致原序列信息的损失。事实上，随着协整理论的发展，对于非平稳的时间序列，可以直接建立VAR模型，确立模型最佳滞后期，再进行协整检验。

首先，在建模时需要明确变量，本文是考察经济与中等职业教育的关系，故选取三个经济指标LNTGDP、LNCZ、LNNC以及一个教育指标LNZXRS作为变量。其次，需要确定最佳滞后期，最佳滞后期的选择既要保证参数有较强的解释力，可以完整反映模型的动态特征，又要考虑模型足够的自由度（滞后阶数越多，模型自由度下降），还需要保证残差不存在自相关。最佳滞后期通过相应的LR统计量和FPE、AIC、SC、HQ信息准则来确定，结果见表4，FPE、AIC、SC、HQ的值均在滞后期为1时最小，故VAR模型的最佳滞后阶数确定为1。

（六）协整检验

由于各变量的时间序列是非平稳的，并且各个序列是二阶单整，故考虑利用协整检验进一步分析西部地区的人均GDP、城镇居民人均可支配收入、农村居民人均纯收入和中等职业学校在校生数之间是否存在长期均衡关系（协整关系）。时间序列对协整关系的检验通常有两种方法，一种是Engle-Granger两步法，另一种是Johansen协整检验法。前者适用于两变量模型检验，后者适用于多变量模型检验，故本文选用适合多变量模型的Johansen协整检验法对LNTGDP、LNCZ、LNNC、LNZXRS四个变量进行协整检验。

VAR是无约束的，而协整是有约束的，协整检验是对无约束VAR模型进行协整约束之后的VAR模型，因此协整检验的最佳滞后期通常是VAR模型的最佳滞后期减去1。由于VAR模型的最佳滞后期为1，所以得到协整检验的最佳滞后期为0。运用Johansen极大似然估计法对相关变量进行协整检验，检验结果见表5。

由表5可知，特征根迹检验与最大特征值检验结果均表明，在5%的显著性水平下，LNZXRS，LNNC，LNCZ，LNTGDP四个变量至少有3个协整关系，即中等职业学校在校生数与农村人均纯收入、城镇人均可支配收入、人均GDP之间存在长期的动态均衡关系，协整结果见表6。

由表6的协整方程结果可知，在长期关系上，中等职业学校在校生数每增加1%，人均GDP增加1.781%；中等职业学校在校生数每增加1%，城镇居民人均可支配收入增加1.395%；中等职业学校在校生数每增加1%，农村居民人均纯收入增加1.532%，此结果验证了假设H3成立。

（七）格兰杰因果关系检验

以上协整分析表明，变量之间存在长期的稳定关系，这只是从数量上得到的结论，但不能确定变量间是否有因果关系。所以，为更进一步研究变量之间的关系，需要进行变量间的因果检验，本文使用格兰杰因果检验法对变量间的关系进行检验。检验结果见表7。

由表7可知，在最佳滞后期为1，显著性水平为5%的情况下，原假设“LnNC不是LnZXRS的格兰杰原因”的F统计量为0.52698，其p值0.4778大于临界值5%，因此不拒绝原假设，说明农村人均纯收入不是引起中职在校生数变化的格兰杰原因。同样在5%的显著性水平下，原假设“LnZXRS不是LnNC的格兰杰原因”的统计量为11.5696，其p值0.0034小于临界值5%，因此拒绝原假设，说明中职在校生数变化是农村人均纯收入变化的格兰杰原因。同理可知，城镇人均可支配收入变化和人均GDP变化均不是引起中职在校生数变化的格兰杰原因；反之，中职在校生数变化是城镇人均可支配收入变化和人均GDP变化的格兰杰原因，即进一步验证了协整方程所得结论的合理性，同时验证了H1不成立、H2成立。