记录数数过程与结果 形成数学知识与经验

编者按：

《义务教育数学课程标准（2022年版）》强调数与运算的结构化与一致性。践行数的运算本质上的一致性，形成运算能力和推理意识，需要从学生知识学习的源头开启研究。以下一组文章以小学生认识数的起始单元为例，基于数数过程与结果，让学生逐步形成数学知识与经验，以整体设计视角探索学生从“自然数”的数量累计到数码直接记数，再到十进位制记数等过程，并在“分与合”的实践中使学生形成数的认识与加、减法的有机联系，以期为大家提供一种借鉴。

摘要：以人教版教材“5以内数的认识和加减法”为研究对象，通过梳理和理解教材的编排特征，基于数的起始认识，立足“计数单位”大概念理解，反思和重构单元学习的路径设计，进行实践同时检验新学习路径的可行性，从而更好地践行数与运算的结构化与一致性。

关键词：小学数学；数学运算；5以内数的认识和加减法

“5以内数的认识和加减法”是人教版教材一年级学生第一次系统地认识数与加减法运算。我们通过对教材编排内容梳理，让学生认识5以内数与相应的加减法；再结合课程标准中关于“数与运算”一致性的要求，对教材中现有的教材编排进行反思；最后结合反思对本单元的学习路径进行重构并进行相应的教学实践。

一、梳理———理解教材的编排特征

把数的认识与加减运算编排在同一个单元中，有利于体现“数与运算”的一致性。但在教材编排中，是否真正体现了一致性？笔者进行了如下梳理：

（一）先认数后运算分层学习

通过整体梳理发现，人教版教材把数的认识与加减法分作两个独立部分进行教学（见表1）。

从上表发现，把“5以内数的认识”分成“1-5数的认识”与“0的认识”两个部分。“2-5”加法和减法的运算则在这两次“数的认识”的中间，“0的认识与加减法运算”安排在同一个课时中作为本单元的最后一课时。

（二）分步学习数的认识

进一步梳理，我们发现“数的认识”的编排特色是“分步学习”，包含数的读写、基数的含义、序数的含义、数的大小比较和数的组成五个学习内容[1]。除第五课时外，每一个课时都是围绕“数的认识”的一个或两个学习内容展开的。

第一课时主要学习“基数的含义”与“数的写法”。基数的含义是通过“数数”发现各种“农家小院”中的狗、鹅、燕子等事物在数量上的特征，分别用对应数量的小棒和数码进行表示，并在“日”字格中学习1-5数的写法（见图1）。小棒表示相应的数量时，3、4、5分别用搭成的三角形、四边形与五边形表示。教学时，我们把它们用表示“2”的方式，从左往右摆放并先让学生用小棒表示数量，再用数码表示。

第二课时学习数的大小比较。教材创设猴子吃水果的情境，通过猴子数量分别与桃子、香蕉和梨的数量的比较中，分别概括出“相等”“小于”和“大于”这三种大小比较的情况，并学习分别用“=”“<”和“>”表示。这里要特别注意，没有直接用不同的水果比较大小，而是依据“小猴吃水果”的故事情境，用小猴的数量与3种水果的数量分别比较大小，这也是本单元比较数的大小创设异质事物情境的特点。

第三课时学习“第几”，即学习序数的含义。教材创设“小明排队”的情境。其中有个“小明排在第几个”的问题，与其他的3个问题比较，它表示的是一个顺序，而其他的3个问题表示的是总和。这样的编排显然是考虑学生在比较的过程中认识到“几”和“第几”含义的差异。同时，在这样的表达过程中，也复习与应用了第2单元中“位置”的学习知识。

第四课时与第五课时学习2-5数的分与合，分成2-4数的分与合、5的分与合。教材回归“农家小院”的具体信息，提出“分一分”的问题，在具体的操作活动中学习2-5数的分与合。显然，数的分与合，与后续学习的加法与减法有着十分重要的联系，是加法与减法含义的原型，更是加法与减法运算的算理与算法。

（三）加法与减法依次学习

加法与减法是四则运算最基本的两种运算。在数数的过程中，如果我们分组数数，再把两组数的结果合并起来，就是加法。如果从数的总和中去掉一部分，即往回数数，求剩下部分的数，就是减法。

人教版教材创设“合并”与“去掉”的情境，分别学习用加法与减法表示，从而学习加法与减法的含义，接着再用数数与数的组成两种方法学习加法与减法的运算。具体教学时，把加法与减法分成两个课时教学，第一课时学习加法的含义与运算，第二课时学习减法的含义与运算。

在加法的含义学习中，教材创设两只手里面的气球合并到一起的主题图，认识加法中“合并”的含义，并用图示对比让学生体会加法左边是3和1的合并，右边的4表示把两个数合并后得到的数。同时，在加法运算的学习中创设两只松鼠跳跃到另一棵树（原有3只松鼠）上，理解“5”是由两个加数运算得到的，分别用数数与数的组合得到结果。与加法的含义和运算的两个情境图相对应，教材创设含义正好相反的情境图，用“放飞”气球表示减法的含义，用“跳走”表示减法的运算。

（四）整体学习0的认识和加减法

“0”与数“1-5”相比，既具有相同的特征，又具有其独有的特点。从基数的视角，0表示没有，从序数的视角，0表示起点。进行大小比较，0比1还要小，从加减法运算的视角，与其他数进行加减运算，也有一些特殊的规律。因此，本课教学设计利用原有的“数的认识”与“加减法运算”的活动经验，创设具体情境，让学生自主归纳出0的特征与加减法运算规律。

教材分别创设“小猴吃桃”和“尺子上的刻度”两个情境，让学生在与已经学习的1-5数的相应特征的比较中，认识到当猴子把2个桃子全部吃完时，盘子里没有桃子了，就用“0”表示，形象地认识到0表示“没有”。“尺子上的刻度”从左往右观察上面的数，分别是0、1、2、3、4、5，直观地认识到0表示“起点”。借用尺子刻度认识0表示序数的含义，有其独特的意义。因为与后面的1、2、3、4、5相比，它在这里的含义相对单一，后面的1、2、3、4、5，不仅表示序数的含义，还包含着基数的含义。如“1”还表示从0开始的长度是1段，依次类推，“2”表示从0开始的长度是2段……

0的加减法运算包括加减运算中出现0和结果等于0两种情况，依据这样的思路，有0的加减法运算可以有如下的几种情况：（1）a+0=a，（2）0+a=a，（3）a-0=a，（4）a-a=0。其中第1、2题可以合并成一类：一个数加0等于原数。减法中的有两类，分别是：一个数减去0等于原数；两个相同的数相减等于0。教材编排的例题与后面的“想一想”，正好对应上述三类有0的加减法运算。

二、反思———指出可以改进之处

小学数学整体构建教学是基于数学知识的内在系统关联和学生的已有认知基础[2]。通过梳理，我们从适度整合、体现一致的要求，提出可以改进的地方。

（一）基于数数可适度整合数的认识

本单元数的认识分成两个阶段，一是1-5数的认识，基本采用“一课一得”的形式编排；二是0的认识，编排在本单元的最后。把0编排在1-5数的认识之后教学，凸显了0的独特性，但在认识1-5数时却变得不全面。因此，可以把0的认识与1-5数的认识整合到一起，使得对基数、序数与大小比较的学习更加完整。

数的大小与序数整合到一个课时中，让学生从基数的大小比较与从大小排列的顺序进行比较，体会到几与第几之间的差异。由于学生已经对5以内数有了一定认知基础，教学中更加侧重基数含义与5以内数的全面性认知，具体将0-5数的认识新授课整合成两课时（见表2）。

这样的整合，不是简单地把几个课时的内容进行叠加，而是为了更好地体现知识之间的内在联系。

（二）数的组成和加法意义实现同构

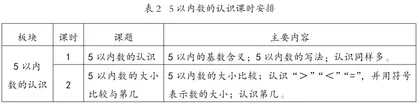
在整体设计时，我们尝试把数的组成作为加法含义的基础，即加法的表达形式就是数的分与合的表达形式。基于此，在学习2-4数的分与合之后，教师选择其中的一个数的分与合的表达形式，书写出加法的两种表达形式，让学生寻找两者的联系，从而认识到加法的表达形式就是数的“合”关联的表达形式。

在学生已经会用连线的方法表示4的分与合，教师一边读“4可以分成3和1”，一边板书：4=3+1，然后让学生说一说这个式子与连线图的异同。接着让学生用读加法算式的方法读一读，并说明“加号”及它的含义。同样的方法认识“3+1=4”。最后比较两个算式的相同点与不同点，并说明加法一般用右边的形式（3+1=4）表示，侧重让学生感知“加法表示合并”，是对数的“合”关联的数学表达（见图2）。

（三）加减运算形成共同思维方式

减法是加法的逆运算。同样的一个情境，加法与减法的含义正好相反。如“3+1”中的“+”表示“合并”，而“4-1”中的“-”表示“飞走”。基于这样的思考，在学习减法时，这样的应用自然就成为了“5的认识与减法”这一课时的学习思路。

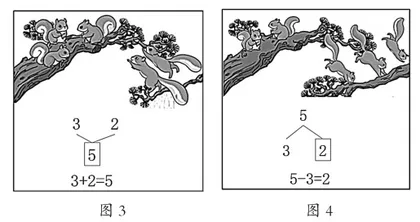
具体地，先出示情境图（见图3），请学生用连线图与加法表示出过程与结果。接着，再出示如图4的情境图，请学生结合图示说一说与图3中的图有什么不同？依据学生的回答，先用连线图表示出含义，接着出示减法算式，请学生对照连线图，说明减法算式中每一个数与符号的含义。通过不断地情境变式，丰富例子，完善5的分与合，并结合图示进一步学习有关0的加减法。

这样，把数的组成与加减法进行有机整合，把加法作为数的组成的表示形式之一，把减法作为加法的逆运算，并且也纳入数的组成之中。形成两个课时的教学内容（见表3）。

三、实践———体现数与加减的融合

通过反思，重构本单元的新知学习序列，为具体实践提供了很好的学习路径。那么，在具体实践中又需要注意哪些要点呢？

（一）经历数数认识5以内的基数

5以内数的认识中也包括0的认识。先结合数数、分类与小棒表征等策略感知1-5数的含义，再通过课件演示、示范与练习学习1-5数的书写，接着再动态演示递减数数得到0，认识到0表示没有，并学习它的书写方法。

1.多元表征认识1-5数的基数含义

出示图1的“农家小院”情境图，请学生说一说图中有什么。学生说出名称，教师圈出相应的内容后，教师追问：数一数它们各有多少。根据学生数数，教师分别用板贴展示（见图5）。这里特别注意玉米图，用串作计量单位，表示1串玉米，是把几样东西看成一个整体，依据这样的思路，再让学生举例子，哪一些地方还用到这样的“1”。学生指出“1个组”“1个班”“1个学校”都是“1”。