有效表征 高效分析

摘要：归一应用问题教学的难点是分析数量关系。现实教学中，归一应用问题数量关系分析得不到应有的重视，主要体现在分析数量关系的方式方法比较单一，设计的活动和引导问题不够细化，造成学生尤其是基础薄弱学生理解比较困难。实践表明，采用“题图结合，分析关系；画出题髓，渐明关系；数归其位，列表入里；细嚼数味，万数互联；句意转换，建联沟通；精准铺垫，分合沟通”分析方法，对帮助各层次学生解决正归一应用问题有较好的效果。

关键词：小学数学；正归一问题；买碗问题；数量关系

归一问题，根据解题的不同步骤，可分为正归一问题和反归一问题。先求出单一量，再用乘法求若干个单一量的归一问题，叫正归一问题，或直进一次归一。先求出单一量，再用包含除法求出含有多少个单一量的归一问题，叫反归一问题或返回一次归一。根据求“单一量”的步骤的多少，可以分为一次归一问题和两次归一问题。倍数问题的一份数、行程问题的速度、工程问题的工作效率、分配问题的一份数、分数问题的每一份等问题，都与归一问题有关。归一问题是小学阶段复杂应用题中的一种重要类型，是由一步应用问题过渡到三步及以上应用问题的重要桥梁。作为典型的乘除整数应用题，是今后学习小数、分数和方程应用问题的重要基础。因此归一应用问题的教学对学生小学、初中乃至高中的应用问题学习有着重要的影响。

归一应用问题教学的难点是分析数量关系。正归一应用问题是归一应用问题最基本的类型，其数量关系分析方法，对归一应用问题乃至其他应用问题有着重要启示和借鉴作用。现在《义务教育数学课程标准（2022年版）》更加关注对数量关系的理解，问题解决不是一个简单的题型训练，也不仅仅是获得解题结果，解决问题≠解题，而是帮助学生学会“怎样想问题”“怎样分析数量关系解决问题”[1]。下面以现行人教版三年级上册的例8“买碗问题”———买3个碗18元，照这样计算，买8个碗多少元？为例，谈谈正归一应用问题分析数量关系的六个基本方法。

一、题图结合，分析关系

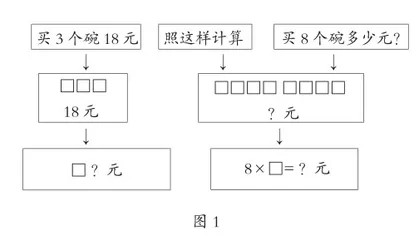
（一）强调对应。即从题意中一步一步地画图，一步一步地根据图来思考、分析关系。把解题思路在用图释题，表征关系中辨明思路（见图1）。

（二）看图分析。从关键句的图示中，明晰可求出单一量，从末尾句的图示中，明晰要求出问题，必须先求单一量。从而从两图的解读中，找到前后的关联（见图2）。

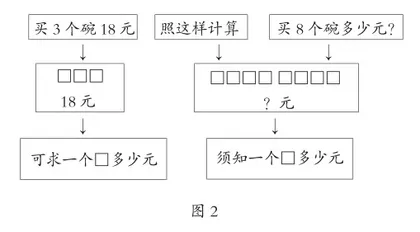
（三）基本关系式。用图画出题意后，思考每一幅图所涉及的基本关系式，或可以写成怎样的关系式。前后两幅图所写出的关系式，是否有着关联。进而理解关系，得出思路（见图3）。

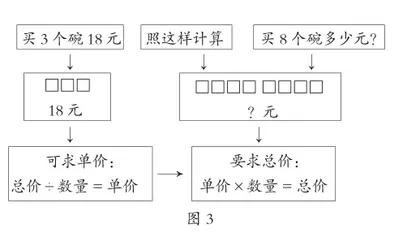
引入常见的数量关系，运用这些数量关系解决实际问题是培养学生问题解决能力的重要途径，小学数学中的数量关系有两个基本的模型：一种是总体等于部分的和，另一种是乘积模型，总价=单价×数量和路程=速度×时间是基本的乘积关系的模型[2]。可见，用基本数量关系式思考问题对解决问题的意义。

二、画出题髓，渐明关系

面对一道应用问题，让学生说一说题目讲了一件什么事情、有哪些条件、要求什么等，这仅仅是表层审题。解决问题依靠理解题目条件与问题的关系，找到重要的等量关系，这需要进行里层审题。而要进入题目之“骨髓”“灵魂”，画图是一种被广泛使用的行之有效的方法。人教版配套教师教学用书在“编写意图”中明确指出，“例8：教学利用画示意图分析数量关系的解题策略”。

画图的目的是为了更好地直观地表征题意，看出数量关系，是分析数量关系的重要方式。有的学生不会做或无从下手，可以尝试画图进行分析，从中寻找解题的突破口。有的学生能够直接列式，教学时，可让学生画图解释算式的含义。

教学时，提供学生的示意图和线段图作品（见图4-7）清晰明了。

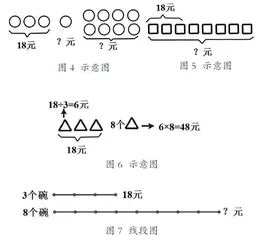
画图策略的重要要求是画得明。具体来说包括齐全（条件、问题）、直观（一眼看明）、正确（符合关键词）、互译（据图说文、据文说图）。但面对存在差异的学生，往往表现出不同的水平层次。

水平1：主要画实物图、简单的符号替代图。做到正确、完整地画出题意。

水平2：主要画示意图、直条图。做到规范、完整地画出题意。

水平3：主要画线段图。能完整地有创意地画出数量关系，做到正确且明理。

这三种水平，可能在同一节课呈现，也可能是不同学生在不同阶段的表现，无论如何，这体现了由繁到简，由粗到精的学习过程。面对水平层次不一样的方法，教学时，需要教师引导学生理解同学的方法并进行优化，促使学生由知一法能知多法，从多元方法习得优化方法。实际上，这些层次不同的方法，在解决后续学习的不同应用问题时，都各有其价值，因此，要发挥好这些课堂上生成的学生资源。

三、数归其位，列表入里

教学时，用类似表格法的方法表示，如“3个18元，8个？元”，这两个信息分两行呈现，与学生一起分析数量关系。

或用列表法分析（见图8）。

这是一个被简化的表格，表格中的数据之间有着对应关系。因为学生没有亲自经历表格简化的过程，因此有部分学生看不懂、弄不明其中的关系。要让学生完全理解表格反映的数量关系，找到解题的思路，有必要让学生回到最初的问题：这个简化的表格，最开始应该是怎样的呢？

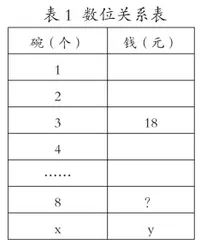
教师可以给出下表，让学生根据题目意思来填，即在3个碗旁边填“18元”，在8个碗旁边填“？元”。再回答：1个碗的价钱和8个碗的价钱分别是多少？让学生在把数归位的过程中，经历抽象的、经历审明关系的过程。最后再把表格简化出来（见表1）。

还可以在表格下面增加栏目，进一步提出问题，如，根据上表，请回答（1）7个碗的价钱是（）；（2）20个碗的价钱是（）；（3）若x个碗的价格是y，那么y=（）。让学生感受到无论求多少份单一量，只要知道单一量即可。从变化中渗透函数思想，看到什么在变，什么始终不变。以上过程，学生借助完整表格，理解简化表格，深入理解对应联系，对学生解决问题有着重要作用。

四、细嚼数味，万数互联

具体步骤是：第1步，每个数字的意义。第2步，审出“照这样计算”的意思。第3步，审明关键句。第四步，审出数量之间的内在对应关系。

买3个碗18元，照这样计算，买8个碗多少元？

①每个数字的意义。3个表示什么，18元表示什么，8个表示什么，“多少元”表示什么。

②审出“照这样计算”的意思。每个碗的价钱是一样的。

③审明关键句。从“买3个碗18元”，想到什么？

摘要为：3个，18元，8个，？元，列出对应关系为：

④审出数量之间的内在对应关系。

3与18有什么关系？8与“？”有什么关系；

3与8有什么关系？18与“？”有什么关系（在碗的个数存在倍数关系时，这样思考更有意义）。

五、句意转换，建联沟通

主要是根据题意，转换表达，逐步探寻数量关系，建立已知、未知和所求之间的联系，从而得出解题思路。

可执已知“条件句”这一关键句追溯得到问题答案（见图9）：

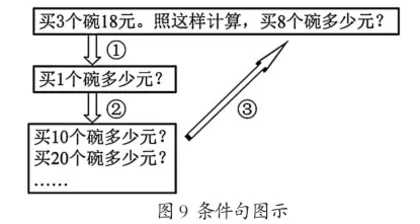
可执“问题句”这一关键句用分析法推理（见图10）：

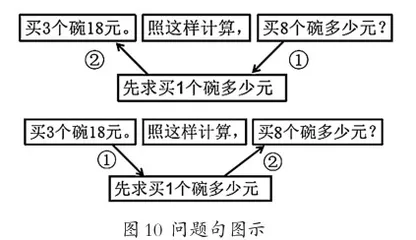
可同时执“条件句”和“问题句”这两个关键句加以分析推理（见图11）：

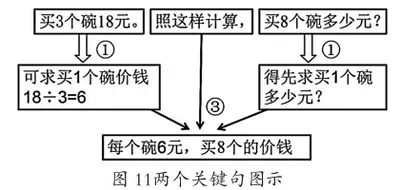
还可以是这样的思路（见图12）：

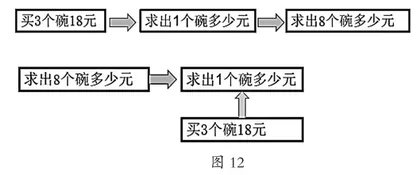
或如下思路（见图13）：

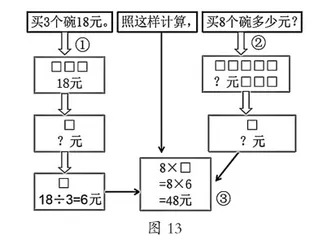
从以上分析，得到一个启示：中间问题是怎么逼出来的？

（一）从问题逼出。求8个碗的价格，自然想到要先求1个碗的价钱。已知条件“买3个碗18元”能求得1个碗的价钱吗？

（二）从条件逼出。条件“买3个碗18元”可以求出吗？（1个碗的价钱）这对解决问题有帮助吗？

（三）从基本数量关系式逼出。题目中的“3个碗”与“18元”分别是数量与对应的总价，“8个碗”与“多少元”分别是数量与对应的总价。由“按照这样计算”和“单价×数量=总价”，可知“1个碗的价钱”是前者可求、后者要求的。

六、精准铺垫，分合沟通

正归一应用问题，常常由两个一步计算应用问题组合而成。因此，教学时，可作“一步转化为两步”（“合”的方法）或“两步转化为一步”（“分”的方法）的复习，让学生对正归一应用问题的结构、题意和解决方法有更为清晰和深刻的理解，同时，能够更好地迁移解决一步计算应用问题的经验运用于新知的探索。

第1类：简单一步计算问题。1.设置连续两个问题。买3个碗花了18元。（1）每个碗多少钱？（2）8个碗多少钱？2.设置有关联的两个问题。（1）学校买3个书架90元，每个书架多少元？（2）每个书架30元，买5个书架要多少元？

第2类：变式。1.变条件（顺向）。（1）1个碗6元，买同样的8个碗，需要多少钱？（2）2个碗（）元，买同样的8个碗，需要多少钱？（3）3个碗（）元，买同样的8个碗，需要多少钱？2.变条件（逆向）。（1）3个碗18元，买同样的1个碗，需要多少钱？（2）3个碗18元，买同样的2个碗，需要多少钱？（3）3个碗18元，买同样的（）个碗，需要多少钱？

第3类：补条件、补问题。（1）3个碗18元，买同样的8个碗，需要多少钱？（2）3个碗18元，买同样的（）个碗，需要多少钱？

学生的学情存在差异，以上方法，为不同层次的学生学习正归一应用问题提供可操作性的方法。学生可以根据自己的情况、教师可以根据学生的实际，灵活地选择其中的方法开展学习和教学活动。

参考文献：

[1] 马云鹏，吴正宪.《义务教育数学课程标准（2022年版）》案例式解读（小学）[M].上海：华东师范大学出版社，2022：96.

[2] 教育部基础教育课程教材专家工作委员会.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012：157 158.

编辑 杨馥毓