感悟，解题策略教学的重要环节

【摘要】在数学教学中，解决问题的教学是非常重要的内容，学生对于解题策略的探索与感悟是否深刻，将直接决定学生能否将解题策略灵活应用到实际中。因此，教师在解题策略教学中应注重引导学生从不同角度思考问题，从而培养学生对解题策略的感悟能力和综合应用能力。

【关键词】数学教学；解决问题；解题策略

解决问题是贯穿在所有数学学习之中的一项重要内容，解决问题的策略可以理解为解决问题的计策与谋略。对解题策略的感悟是策略教学至关重要的一环，其中，“解决问题”只是教学的媒介，“感悟策略”才是教学的核心。

在苏教版小学《数学》三年级（上册）77页出现这样一道习题：“小玉家养鸡和鸭一共54只，卖掉20只鸡后，鸡和鸭的只数同样多。她家原来养鸭多少只？养鸡多少只？”这道题追根溯源是一道和差问题，而教材正式出现和差问题是在四年级（下册）第五单元的例1：“小宁和小春共有 72 枚邮票，小春比小宁多 12 枚。两人各有邮票多少枚？”

对比这两道题，虽说第一题属于和差问题的范畴，但它又异于四年级的和差问题，不像传统的和差问题那样复杂。根据学生学情，教师肯定不能用四年级和差问题的教学思路。一方面学生难以理解，另一方面也违背了教材的课程安排。为此，根据多次教学实践，可以总结出两点教学建议：

一、从条件出发分析和解决问题

苏教版小学《数学》三年级（上册）“解决问题”单元的内容是《从条件想起》，因此，本单元的重点内容是掌握从条件入手的解题策略，这道习题清晰体现了这一方法的优势。由于学生在低年级的学习中，对于“一共的只数-卖掉的只数=还剩的只数”这一数量关系已经非常熟悉了，所以看到题目中“小玉家养鸡和鸭一共54只，卖掉20只鸡”的表述，他们马上想到根据这两个条件可以求出“还剩多少只”；而“卖掉20只鸡后，鸡和鸭的只数相等”这一条件的含义是，从54只鸡和鸭中去掉20只鸡后，剩下的34只鸡和鸭中，鸡和鸭各占一半。因此，学生可以依据这里的条件顺理成章地解题。按照从条件入手的策略，解题步骤可以是：先利用“鸡和鸭一共54只”和“卖掉20只鸡”两个条件，求出剩下的数量；再根据“剩下的鸡和鸭数量相等”这个条件，推算出原本鸡和鸭的数量：

现在一共多少只：54-20=34（只）

原来的鸭：34÷2=17（只）

原来的鸡：17+20=37（只）

答：原来的鸭有17只，原来的鸡37只。

从学生对数量关系的理解和掌握程度的学情出发，像这样从条件出发分析和解决问题，不仅符合学生的思维特点，也提高了他们对“从条件想起”解题策略的运用能力，让学生在自己原本的思维模式上进行再生长。当然，这道题同样也是一道“和差问题”，学生在解决“和差问题”时，容易犯一个常见的错误：

原来的鸭：54÷2=27（只）

原来的鸡：27+20=47（只）

答：原来的鸭有27只，原来的鸡47只。

学生出现这样错误的解答过程，到底是为什么呢？首先，学生对于已知条件之间的联系并不清楚，即对“从条件想起”的策略掌握并不扎实。其次，学生在之前的学习中对于数量关系的理解还不深刻，这也造成对策略的感悟十分困难，因此教师在平时的课堂中应当加强训练，锻炼学生运用“从条件想起”的策略并完整地表达解题思路的能力。有了“从条件想起”这一解题策略的支撑，学生在完整的思路表达中更容易形成缜密的思维方式，这也为今后用不同方法灵活解决“和差问题”提供了学习基础。

二、使用不同方法辅助思考

事实上，我们在解决问题时，不应当局限于一种方法。尽管教材并没有要求学生必须用不同方法解答，但是有经验的教师往往会在这些地方适当放慢教学节奏，尽可能启发学生从不同角度展开思考。因为，这样做不仅有助于丰富学生对基本数量关系的理解，也有助于培养学生的求异思维，从而尽可能大的发挥习题的教学价值。

苏教版小学《数学》三年级（上册）“解决问题的策略”例2中，教材为了帮助学生理清题中的条件和问题，就以线段图的方式直观呈现了三种花数量之间的关系，帮助学生初步积累借助图形进行分析和思考的经验，因此，还有些学生想到了画线段图来解决此题。

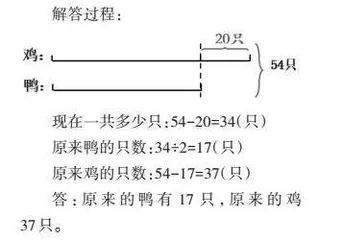
解答过程：

现在一共多少只：54-20=34（只）

原来鸭的只数：34÷2=17（只）

原来鸡的只数：54-17=37（只）

答：原来的鸭有17只，原来的鸡37只。

虽然列式解答的过程与运用“从条件想起”的策略基本一致，但其思维深度是不同的。借助线段图，学生可以很清晰地理解：虚线左侧是鸡和鸭同样多的部分，右侧是鸡比鸭多出的部分。只要从总数里面去掉多出的部分，就可以得到两份鸭的只数，从而求出原来鸭有多少只，鸡有多少只，整个思路过程也便于学生理解。

有些学生在看到线段图后，还联想到其他解题方法。根据“卖掉20只鸡后，鸡和鸭的只数相等”这一条件，可以推理出“鸡比鸭多20只”或“鸭比鸡少20只”。通过运用假设法，同样可以解决这道题：

假设增加20只鸭，这时鸡和鸭同样多。

现在一共多少只：54+20=74（只）

原来鸡的只数：74÷2=37（只）

原来鸭的只数：37-20=17（只）

答：原来养鸡37只，原来养鸭17只。

可以看到，当教师给予学生充分的探索空间时，学生的思维迸发出了更灿烂的火花。有了“从条件想起”这一解题策略的支撑，有的学生想到了画线段图解决问题的方法，教师合理运用图示，充分发挥线段图在理解和应用策略中的作用。看到线段图，有的学生运用了假设法再次解题，学生初步体会到了解决问题策略的多样性与综合性。在课堂上合理使用不同的方法辅助思考、分析、解决问题，学生思维得到了充分的启迪，这不仅帮助学生感悟不同策略的应用价值，也提高了他们对解题策略的灵活运用。“解决问题的策略”教学并不是简单地、单一地给学生讲授某种解题方法，而在于着重培养学生对策略的感悟、理解和应用能力。有了运用不同策略解决实际问题的解题经验，学生对解题策略的理解和感悟再也不是单一的、有局限性的，而是发散的、多样的，对解题策略的综合应用能力才能有质的提升。

教材将这道题安排在此，意在启发教师在教学“从条件出发”或“从问题出发”解决问题时，引导学生根据问题特点灵活运用画图、列表、假设等方法灵活解题。这样既帮助学生积累丰富的解题经验，也为后续四年级下册学习画线段图解决复杂的“和差问题”做好铺垫。

总体而言，“解决问题的策略”教学应以理解数量关系为基础，注重探索与比较解题思路，强调策略间的互补与配合，引导学生在回顾中积累经验、在反思中提升理解，从而不断增强感悟、理解和应用策略的能力。

（作者单位：王伟，江苏省丹阳市埤城中心小学；张莉，江苏省丹阳市华南实验小学）