利用GeoGebra软件，实现动静转化

摘 要：教学苏科版初中数学八年级上册第六章《一次函数》时，可以在学生学习了一次函数的定义、图像和性质，明白了各项系数的含义，能根据表达式画出图像，也能根据图像分析性质，初步感悟了数形结合思想的基础上，设计一节拓展课，引导学生控制变量逐个研究，循序渐进从单一到综合，利用GeoGebra软件的动态几何功能，研究含参一次函数的图像与性质并进行简单的应用，帮助学生深入理解参数的意义和作用以及参数与函数图像之间的关系，重点感悟动静转化、“变与不变”等思想。

关键词：初中数学；含参一次函数；动态几何软件；动静转化

一、 教前思考

“含参函数的图像与性质”是近些年中考的热点。因为含有参数，含参函数不仅具有表达式的抽象性，而且具有图像的动态性。从教学实践来看，不少教师直接让学生观察函数图像、记住相关结论，套用解题模型。这使得学生没有经历知识发生、发展的过程，难以理解数与形的变化规律，无法灵活地运用知识解决问题。尤其是对图像的运动变化，教师不知如何言传，学生不知如何意会。

《义务教育数学课程标准（2022年版）》指出：“教师可以利用数学专用软件等教学工具开展数学实验，将抽象的数学知识直观化，促进学生对数学概念的理解和数学知识的建构。”［1］GeoGebra是一款优秀的动态几何软件，操作简单、交互性强，能够瞬时进行数式运算，作出相应图形，并同时呈现、随意改变“数”与“形”，可以降低学生认识的难度，帮助学生多角度思考函数中参数的意义和作用，并提高教学效率。

因此，教学苏科版初中数学八年级上册第六章《一次函数》时，可以在学生学习了一次函数的定义、图像和性质，明白了各项系数的含义，能根据表达式画出图像，也能根据图像分析性质，初步感悟了数形结合思想的基础上，设计一节拓展课，引导学生控制变量逐个研究，循序渐进从单一到综合，（手持平板电脑）利用GeoGebra软件的动态几何功能，研究含参一次函数的图像与性质并进行简单的应用，帮助学生深入理解参数的意义和作用以及参数与函数图像之间的关系，重点感悟动静转化、“变与不变”等思想，同时积累研究含参函数图像与性质的经验，为后续研究含参反比例函数、二次函数等的图像与性质奠定基础。

二、 教学过程

（一） 引参数之问

问题1：同学们，我们对一次函数y=kx+b（k、b为常数，k≠0）的图像与性质已经有哪些认识？

追问：k与b的不同取值在图像上会体现出不同的特征，如果它们是不确定的常数，也就是参数，我们又该如何研究呢？

问题1引导学生复习一次函数的图像和性质，初步感受系数k与b与图像（直线）、性质的联系；追问则激发学生思考如何研究参数k与b不确定的问题，点明本节课的研究内容。

（二） 明参数之意

探究1：你能画出y=2x+b（b为常数）的图像吗？请先手工操作，再利用Geogebra软件操作。说说你的发现。

探究2：你能画出y=kx+2（k为常数，k≠0）的图像吗？请先手工操作，再利用Geogebra软件操作。你有哪些发现？

追问：你是如何理解参数的？这两个函数表达式有何特点？

两个探究活动分别控制一个参数不变，让另一个参数可变，引导学生关注参数变化与图像变化之间的关联。学生可以分别赋予b与k不同的数值，再描点作图。在探究1的作图中，学生会得到一些互相平行的直线，可能发现：当b不断变化时，图像在做平移运动；在探究2的作图中，学生会得到一些

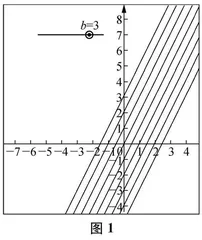
经过点（0，2）的直线，可能发现：当k不断变化时，图像在做旋转运动。在此基础上，学生可以利用Geogebra软件分别创建b和k的滑动条，动态呈现直线（图像）平移和旋转的过程（图1、下页图2所示分别是平移和旋转过程中的一个“瞬间”），真正打通从静到动（从多条直线平行到一条直线平移、从多条直线经过一点到一条直线旋转）的认知障碍，进一步感悟动静转化、“变与不变”的思想。

追问激发学生基于作图的经验，思考参数的意义，感受参数变化与图像变化的关联，体会数与形之间的动与静，培育动态变化的数学眼光。同时，引导学生关注含参函数表达式的结构，抽象出一次项系数含参和常数项含参两种情况，为探究3做好铺垫。

（三） 寻参数之联

探究3：

根据含参一次函数y=kx+b（k、b为常数，k≠0）表达式的特点，你还想研究哪些特殊的含参一次函数？请写出它们的表达式。

追问1：它们的图像有什么特点？小组交流后，利用Geogebra软件操作、展示，说说你们的发现。

追问2：以y=kx+k（k为常数，k≠0）为例，你能证明该一次函数的图像经过定点（-1，0）吗？

追问3：若一次函数的图像经过定点（3，0），你能写出它的表达式吗？

设置开放性的探究活动，引导学生从“数”的角度思考一次项系数的参数、常数项的参数之间可能存在的关系：相等关系、倍数关系、互为相反数、互为倒数、互为负倒数等。追问1激发学生“由数想形”，借助Geogebra软件动态呈现函数图像（图3所示是一个“瞬间”），得到一些特殊的结论（如表1所示）。追问2引导学生从代数推理的角度证明其发现，实现从感性认识到理性认识的转变。追问3激发学生“由形想数”，感受函数图像经过定点（3，0）与表达式含有因式（x-3）之间的一致性。整个探究活动促使学生从单一（孤立）地看走向综合（联系）地看，引导学生再一次体会参数对函数图像的作用，感悟动静转化、“变中不变”的思想。

（四） 破参数之术

例题：已知一次函数y1=kx+2（k为常数，k≠0）和y2=x-3。当x＜1时，y1＞y2。结合图像，直接写出k的取值范围。

给出一个含参的一次函数和一个不含参的一次函数，以及它们之间的不等关系，让学生利用本节课学习的含参一次函数的图像和性质，寻找运动变化过程中的临界位置，解决参数的取值范围问题。学生可以基于y1=kx+2的图像是绕点（0，2）旋转的直线，利用Geogebra软件画图，结合所给不等式，找到旋转过程中的两个临界位置（如图4、图5所示），感受变化过程中的特殊情况对解决问题的作用，体会动静转化等思想对解题思路的启发。

（五） 研参数之道

问题2：我们是怎样研究含参一次函数的图像与性质的？

追问：类比含参一次函数，你将如何研究y=ax2+b（a、b为常数，a≠0）的图像与性质？

问题2引导学生回顾所学，归纳研究含参一次函数图像与性质的方法：控制变量，研究单一参数；循序渐进，从单一（孤立）的参数到综合（联系）的参数；数形结合，打通由参数决定的表达式与图像之间的关系；动静转化，打通参数的一般情况与特殊情况之间的关系；“变与不变”，在参数变化的过程中寻找不变的规律；从实验猜想到推理（计算）论证；利用信息技术辅助实现从数到形、从静到动、在“变”中发现“不变”；学用结合，在旧知识的运用中学习新知识。

追问引导学生课后迁移研究含参一次函数图像与性质的经验，研究含参二次函数（从没有一次项的简单情况开始）的图像与性质，体会类比思想，感受研究方法的一致性，进行结构化学习。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版，2022：89．

*本文系江苏省中小学教学研究第十四期课题“基于学科监测数据的‘内向反思式’质量分析区域推进研究”（编号：2021JYJC14-ZB01）、江苏省教育科学“十四五”规划课题“初中数学课程中的代数推理及教学策略研究”（编号：SJMJ/2022/02）、江苏省南京市教育科学“十四五”规划课题“智能技术支持的‘数学+’跨学科项目式学习研究”（编号：L/2022/02/021）的阶段性研究成果。