学术交流反哺“数学物理方程”课程建设

［摘 要］ “数学物理方程”是一门研究生基础课程，该课程以具有物理背景的偏微分方程作为研究对象，具有较强的理论性。提出了除讲授法教学外，还积极采用专题研讨、学科前沿讲座与学术交流等教学方法相结合，以此突出课程的研究性质，发展学生的思维能力，帮助学生建立良好的专业基础，培养他们开展科研工作和解决实际问题的能力。建立线上讲座资源库，供学生反复观看并温故而知新，把讲座短暂的知识盛宴转化为学生长久的成长补给。“数学物理方程”课程建设和研究生培养是个系统工程，学科前沿讲座和学术会议从数学物理方程的基本概念、基本原理和基本问题中挖掘出蕴含的数学思想，并用这些数学思想指导学生去解决数学问题，为学生将来从事数学教学和科学研究打下坚实的基础。

［关键词］ 数学物理方程；科研讲座；专题研讨；学术会议

［基金项目］ 2021年度宁夏回族自治区人才项目“流体力学方程数学理论研究”（21022005105）

［作者简介］ 杨婉蓉（1985—），女，宁夏银川人，博士，北方民族大学数学与信息科学学院副教授，主要从事偏微分方程研究。

［中图分类号］ G642.3 ［文献标识码］ A ［文章编号］ 1674-9324（2025）12-0033-04 ［收稿日期］ 2024-10-13

“数学物理方程”是一门研究生基础课程，该课程以具有物理背景的偏微分方程作为研究对象，根据质量守恒、动量守恒、能量守恒等物理定律推导并建立数学物理方程。通过深入剖析波动方程、热传导方程及泊松方程等模型，阐明和介绍偏微分方程的基本理论和解题的典型技巧，如特征线法、极值原理、格林函数等。其宗旨是为偏微分方程专业方向研究生夯实理论和科学研究基础，培养他们开展科研工作和解决实际问题的能力［1］。

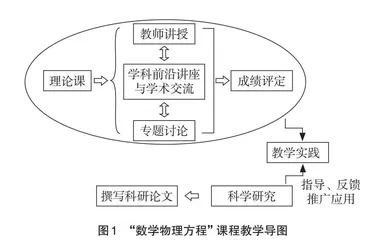
“数学物理方程”是一门极具有挑战性的课程，它把数学理论、研究方法、物理实际三者有机结合，这不仅需要学生具有扎实的数学物理基础，更需要教师在教学中立足于理论与实践相结合，坚持“以学促教，学以致用”的原则，探讨与延伸数学相关理论研究，帮助学生较稳定地形成数学观念，掌握数学方法，提高解决问题的能力［2-8］。考虑到数学物理方程与其他专业课程的内在联系与衔接关系，课程组团队除加强讲授法教学外，还积极采用学科前沿讲座与学术交流、专题研讨等教学方法，以此突出课程的研究性质，发展学生的思维能力，帮助学生建立良好的专业基础，完善专业知识结构，如图1所示。

一、具体案例

1.邀请宜春学院臧教授分别于2022年7月13日—2022年7月28日和2023年7月21日—2023年8月8日访问北方民族大学，其间针对“数学物理方程”课程组织开展了暑期讲习班，采取上午授课结合下午专题研讨的方式进行，主要内容是介绍椭圆方程的极大值原理、Schauder估计、De Giorgi-Nash-Moser迭代，以及Littlewood-Paley理论及其在流体力学方程中的应用等基本理论和研究方法。

2.邀请臧教授于2024年11月21日—2024年11月24日访问北方民族大学，其间做了学科前沿讲座：翼尾的涡线稳定性，报告主要讲解可压欧拉流体绕薄机翼产生涡线的相关机制。通过介绍欧拉流体绕薄机翼的研究背景及研究方法，讲解如何通过拉格朗日坐标变换将方程变换成椭圆方程，进行Schauder估计，构造闸函数以及极大值原理证得翼尾的涡线稳定性理论。“数学物理方程”课程组团队和全体学生都参加了讲座并进行了交流讨论。

3.我们于2024年5月17日—2024年5月20日举办了“非线性偏微分方程”学术研讨会，旨在为我院师生搭建学术交流平台，促进学术合作与学术创新。会议邀请了香港中文大学、武汉大学、美国圣母大学和首都师范大学等知名教授，主要围绕非线性偏微分方程前沿问题组织系列学术报告并开展了相关学术讨论。

4.为了交流非线性偏微分方程及相关领域的新研究成果，为偏微分方程及相关领域的专家学者提供一个探讨交流新研究方向和研究成果的平台，我们于2024年6月14日—2024年6月16日举办了“流体力学研讨会”学术研讨会，会议邀请了30多位专家学者，围绕流体力学中的偏微分方程及数学物理中的偏微分方程组等前沿问题组织系列学术报告开展学术讨论，以寻求新的研究方向和合作领域。

二、案例应用效果

通过对北方民族大学数学与信息科学学院2022级、2023级、2024级数学专业研究生“数学物理方程”课程实行此教学模式，得到效果如下。

1.学科前沿讲座使学生的知识得到了科学实践。例如，专家关于飞机尾翼的涡线稳定性理论讲座，与“数学物理方程”课程内容高度吻合，使学生切实地体会到实际物理背景下守恒律建立方程模型的原理，并对如何利用极值原理求解椭圆方程问题有了直观且深入的理解。通过讲座学生可以接触专业领域新的研究成果、理论观点和实践经验，从而拓宽知识视野和思维方式。讲座经常会有不同的观点和思想激烈碰撞，通过提问和讨论环节，学生的批判性思维和创造性思维得到了锻炼，激发了学生的科学研究兴趣。（摘录几份原稿）“讲座和会议作为课程的延伸，邀请专家分享新科研进展，极大地丰富了我们的知识版图。”“专家的讲座和前沿的研究成果开阔了我们的视野，提升了我们的学习效果和体验。”

2.专题研讨增强了学生的学习能力和科研意识。“数学物理方程”课程内容具有很强的系统性。例如，守恒律建立模型→一维情形初值问题→高维情形初值问题→初边值问题，我们根据知识的逻辑结构和学生的认知水平制定具有针对性、启发性、循序渐进性和探索性的系列问题。学生通过收集和查阅相关资料，围绕这些问题进行自学、讨论、探索。系统掌握数学知识的同时，迫使学生学会独立思考，提升发现问题和解决问题的能力，形成初步的科学研究意识。同时也形成了以师生互动、学生自主探索与合作交流为特征的教学模式。（摘录几份原稿）“在学习的过程中，需要掌握方程的推导和求解，明确其物理内涵与数学表示的关联，专题研讨极大地提升了我的逻辑推理能力和理论联系实际的能力，让我逐渐领略到这门课的精妙之处，也深刻理解了老师说的数学很美的精髓。”“老师在授课和专题研讨中注重理论联系实际，这种教学方式不仅加深了我们对抽象理论的理解，还激发了我们对科学研究的热情，培养了我们应用数学工具解决实际问题的能力。”

3.学术会议提高了学生的学习积极性，激发了学生的科研兴趣，培养了学生的创新意识和创新能力。学术交流使课堂教学更具有前瞻性及理论联系实际，学生由被动接受转变为积极探索和主动获取，激发了学生学习的自主性、能动性和创造性。通过参加学术报告，学生可以更深入地了解专业领域的新动态，扩展知识范围，掌握新的科学技术。在学术交流中，他们与自己研究领域兴趣相投的专家学者交流讨论，特别是对于研究生一年级的学生，能够帮助他们缓解学业迷茫，更快地找到研究兴趣，找准研究方向。

三、案例反哺亮点

1.会议邀请了来自美国圣母大学和我国香港中文大学、北京大学、中国科学院、北京师范大学、南京大学、中山大学、成都电子科技大学、河南理工大学等16所高校及科研院所偏微分方程领域的知名专家学者做报告，为我院师生搭建了学术交流平台，促进了学术交流合作与学术创新，加强了我院数学学科建设。

2.暑期讲习班采用授课和专题研讨相结合的方式，培养学生的自主探索和创造能力，提高了学生的积极性。专题讨论通过系列问题引导法，使学生不仅学到了基础知识，还加强了逻辑思维的训练和科研能力的提升。（摘录几份原稿）“讲习班上老师的课堂思路清晰、环节紧凑、重点和难点突出、设计合理，整节课的各个环节都衔接得恰到好处，每一步推导有理有据，通过板书的形式表现让我们更清楚地理解老师的思路和知识的本质。”“老师对课程内容编排非常精妙，从基础理论的逐步搭建到复杂方程的深入探讨，逻辑严密且思路清晰，最重要的是老师鼓励我们独立思考、探索和解决问题，让我收获颇丰。”

3.通过举办学术会议给我院师生提供了一个交流与合作的平台‌，会议作为“数学物理方程”课程教学的有效补充，丰富了课堂内外的教学资源，使学生可以接触到更深入、更前沿的数学理论和应用，从而扩展他们的专业知识领域‌。同时，会议报告都来自同领域的知名专家学者，他们的专业知识和热情能够激发学生科学研究的兴趣，会议中包含的实践环节，能够帮助学生将所学知识转化为实际操作技能。此外，会议涉及一些新颖的研究成果和独特的解决方法，这对于培养学生的创新意识和创新能力具有积极的作用。特别是对于有志从事数学研究或相关职业的学生来说，会议可以提供未来发展的方向和人脉资源。

4.学术交流和课程教学相互交融，加强了团队建设和人才培育。我们建设了学术梯队，定期开展教学和科研研讨班，促进北方民族大学偏微分方程专业发展，推动宁夏回族自治区优势特色学科“计算数学—生态环境”的建设与培育。培养硕士研究生20余名和博士研究生1名，为民族地区人才培养与储备尽一份绵薄之力。

结语

从实践效果可以看出，学生对学科前沿讲座和学术会议反哺“数学物理方程”课程教学给予了肯定并积极地配合，但也暴露出了一些问题。比如，研究生一年级学生对专业领域了解较少，所以在学科前沿讲座和学术交流中表现得比较胆怯，对于新知识的吸收也不尽如人意。今后我们会不断探索改进，邀请更多的专家开展一些基础性专业知识的讲座，使学生对于新理论和新方法的学习有一个循序渐进的过程，从而达到良好的教学和科研效果。积极参加和举办更多的国内外专业方向研讨会，使我们的学生能够走出去，见识更广阔的学术天地。此外，我们将建立线上讲座资源库，供学生反复观看并温故而知新，把讲座短暂的知识盛宴转化为学生长久的成长补给。

“数学物理方程”课程建设和研究生培养是个系统工程，学科前沿讲座和学术会议从数学物理方程的基本概念、基本原理和基本问题中挖掘出蕴含的数学思想，并用这些数学思想指导学生去解决数学问题，从而把基本概念、基本原理和解决问题的基本思想方法融为一体，使学生形成良好的数学观念，为学生将来从事数学教学和科学研究打下坚实的基础。在此我们真切地希望得到同行的帮助和指导，共同为促进教学研究尽自己的一份微薄之力。

参考文献

［1］姜礼尚，陈亚浙，刘西垣，等.数学物理方程讲义［M］.黑龙江科学高等教育出版社，2007：1-239.

［2］刘肖云.数学物理方程课程教学改革与实践［J］.黑龙江科学，2021，12（7）：122-123.

［3］胡赵胜，林珍华，常晶晶.“以学生为中心”的数学物理方程课程教学方法探索［J］.物理通报，2024（4）：13-16.

［4］王婧慈.工科类“数学物理方程”混合式教学改革探索与实践［J］.科教导刊（中旬刊），2020（11）：129-131.

［5］王桃，郭辉.“数学物理方程”课程教学改革的几点思考［J］.教师，2020（5）：50-51.

［6］牟海宁.新工科背景下“数学物理方程”课程教学改革探索［J］.科教文汇（中旬刊），2020（29）：65-66，72.

［7］贾对红.数学物理方程教学改革与探讨［J］.治学院学报，2020，37（2）：64-66.

［8］耿永才.数学物理方程本科教学改革初探［J］.教育教学论坛，2018（26）：119-120.

Contribution of Academic Exchanges to the Construction of the Course Mathematical Physics Equation

YANG Wan-rong

（School of Mathematics and Information Science， North Minzu University， Yinchuan，

Ningxia 750001， China）

Abstract： Mathematical Physics Equation is a graduate basic course， this course with physical background as the research object， has a strong theoretical feature. In addition to teaching methods， we should actively adopt the combination such as thematic seminars， frontier lectures and academic exchanges， so as to highlight the research nature of the course， develop students’ thinking ability， help students establish a good professional foundation， and cultivate their ability to carry out scientific research work and solve practical problems. It should establish an online lecture resource database for students to review the past and learn the new， and transform the short knowledge feast of the lecture into a supply for students’ long-term growth. The development of course content and graduate training in Mathematical Physics Equations constitutes a systematic endeavor. The lectures and academic conferences within this discipline explore the mathematical thought embedded in the fundamental concepts， principles， and problems of Mathematical Physics Equation. These principles are then utilized to guide students in solving complex mathematical problems， thereby providing them with a robust foundation for future involvement in mathematics education and scientific research.

Key words： Mathematical Physics Equation; research lecture; seminar; academic conference