小学数学序列性教学的内涵意蕴及实施策略

小学数学教学要遵循数学知识的逻辑顺序，要符合小学生的认知顺序，要契合课堂教学的活动顺序。小学数学序列性教学按照从简单到复杂、从具体到抽象、从特殊到一般的序列引导学生学习，这样的序列有助于学生感悟知识之间的联系，促进知识的迁移，构建知识的结构，促进学生核心素养的发展。

小学数学序列性教学是指按照小学生的认知顺序和数学知识的逻辑顺序，有计划、有步骤地组织和实施数学教学活动。小学数学序列性教学有利于促进学生对数学知识的理解和掌握，发展学生数学思维，培养学生的数学核心素养。

一、小学数学序列性教学的内涵意蕴

小学数学序列性教学的内涵主要体现在学生认知发展的序列性、数学知识发展的序列性、教学活动实施的序列性三个方面。

1.学生认知发展的序列性

根据皮亚杰的认知发展理论，儿童的认知是按照“感知运动阶段一前运算阶段一具体运算阶段一形式运算阶段”的顺序发展的。小学生处于具体运算阶段。第一学段更多的表现为动作直观，第二学段倾向于具体形象，第三学段向抽象逻辑发展。小学数学教学要与小学生认知发展水平相匹配，小学数学教学内容的选择和教学活动的设计要遵循学生的认知顺序。教师在教学过程中应充分考虑学生的认知顺序，识别小学生所处的认知发展阶段，按照学生认知顺序组织教学活动，使教学内容和方式与学生的认知水平相匹配，从而促进学生的数学学习。

例如数的运算，根据学生的认知顺序和知识的逻辑顺序，教材在每个年级都安排了不同的学习内容。教学时要循序渐进，基于计数单位、理解算理、掌握算法，发展运算能力。处于具体运算阶段的小学生，一、二年级的认知方式主要是直观动作，三、四年级的认识方式主要是具体形象，五、六年级的认知方式主要是抽象逻辑。一、二年级学习整数的四则运算时，要借助数小棒、分小棒、画图形等直观动作，帮助学生理解计算的算理，感悟“相同计数单位个数的累加”；三、四年级学习多位数的乘除法时，在具体实例探究的基础上，抽象出一般的计算方法；五、六年级学习分数乘除法时，要立足“计数单位”，沟通|感悟“数运算的一致性”，建立乘除法的运算模型（如整数乘除法、小数乘除法和分数乘除法之间的联系，图1）。

2.数学知识发展的序列性

小学数学序列性教学强调教学内容的逻辑性和连贯性，遵循数学知识的自然发展顺序，确保学生能够逐步深入地理解和掌握所学内容。这种逻辑顺序不仅体现在单个课时之内，而且体现在多个课时的单元之内、多个单元的主题之内，甚至跨学科的领域之内。

例如多边形面积的学习，首先学习长方形和正方形的面积，理解面积的度量本质；接着学习平行四边形的面积，体验图形的等积变换，渗透转化思想；然后学习三角形的面积，感悟三角形面积的多种推导方法，发展学生的推理意识；最后学习梯形的面积，对之前学习的推导面积方法进行迁移应用（如图2）。

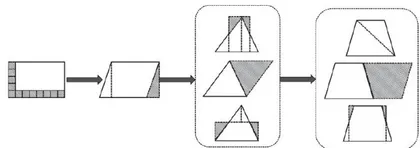
从图2可以看出，长方形面积是学习多边形面积的基础，平行四边形面积是对长方形面积的拓展（先转化再度量），三角形面积是对平行四边形面积的深化（多种转化方法），梯形面积是对三角形面积的迁移学习。这种逻辑顺序能够帮助小学生建立多边形面积的知识结构，促进学生感悟多边形面积之间的联系，加深对平面图形面积本质的理解。

师应根据教学目标、教学内容和学生特点，合理安排教学活动。包括提出问题、合作探究、交流反馈、总结应用等环节的有机衔接和合理过渡，以确保教学活动的连贯性和有效性。在小学数学教学中，序列性学习任务常见的形式有递进式序列任务、发散式序列任务和聚合式序列任务（如图3）。

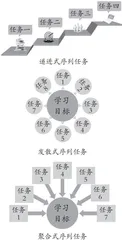
3.教学活动实施的序列性

（1）递进式序列任务。递进式序列任务是线性的，是从简单到复杂逐步增加难度，通过完成一系列任务教学活动实施的序列性指的是在教学过程中，教|逐渐掌握更复杂的技能或概念。它可以帮助学生建立稳定的知识基础，然后在此基础上学习新的知识，有利于从旧知识迁移到新知识，感悟新旧知识之间的联系。如在学习“圆的周长”时，教师可设计如下递进式序列性任务，探索圆的周长与直径的关系：任务一，圆的周长与什么有关；任务二，圆的周长与直径有什么关系；任务三，圆的周长与直径的商在什么范围之内；任务四，圆的周长与直径的商是多少。教师引导学生在层层递进中探究圆的周长与直径之间的关系。

（2）发散式序列任务。发散式序列任务是非线性的，鼓励创造性思维，探索开放性答案。学生可以按照不同的顺序完成序列任务，也可以同时完成两个或多个序列任务。它的答案不唯一，而是要求学习者探索不同的解决方案或观点。这种学习方式的主要优点是结构灵活，可以探索复杂、有深度的知识。如在学习“认识三角形”这个单元时，教师可以设计如下发散式的序列性任务，从不同角度加深对三角形的认识：任务一，三角形的三个顶点的位置关系；任务二，三角形三条边的长短关系；任务三，三角形的三个内角的大小关系；任务四，三角形的底和高之间的位置关系。发散式的序列任务可以从不同角度丰富学生对三角形的认识。

（3）聚合式序列任务。聚合式序列任务通常有一个明确的目标或者预期的答案，强调的是寻找最有效的方法达成目标或者解决问题，可以提高学习者的批判性思维能力。如在学习“分数的初步认识”时，教师可设计如下聚合式的序列任务，促进学生对分数意义的理解：任务一，表示一个圆的二分之一；任务二，表示出一个长方形的二分之一；任务三，表示出一条线段的二分之一；任务四，表示出一元钱的二分之一；任务五，平均分的对象不同，为什么都能表示二分之一。教师通过聚合式的序列性任务促进学生对二分之一数学本质的理解。

小学数学序列性教学中的“序”是多维度和多层次的，既包括教学内容本身的逻辑顺序，也包括学生认知发展的顺序，以及教学活动实施的合理顺序，这三个“顺序”相辅相成，共同构成序列性教学的三个核心，共同促进学生的认知发展，促进学生核心素养的培养。

容和不同的作用，教师可分别采用“因‘生’而序、因‘知'而序、因‘效’而序”的实施策略，优化小学数学教学，促进学生深度学习，培养学生核心素养。

1.因“生”而序，促进认知序列化

同样是小学生，所处的阶段不同，其认知特点也不同。心理学家将小学生的思维划分为直观动作思维阶段、具体形象思维阶段和抽象逻辑思维阶段[2]。在教学中教师要根据学生不同的思维特点展开序列化教学，促进学生认知的序列化

（1）低段学生，在直观操作中应用序列化教学。心理学家皮亚杰说“儿童的智慧在指尖跳跃”3。小学一、二年级学生在学习数学时，主要通过直观操作的方式学习。直观操作不是让学生机械地做、无序地做，而是引导学生充分调动多种感官有序参与认知活动。教师要根据学生的认知特点，引导学生在直观操作中进行序列化学习，让学生的认知感受、认知体验更丰富、更深刻。如在学习1＼～5的认识时，依据学生认知特点，可开展基于直观操作的序列化学习“观察与数数一操作与分类一手势与图形一符号与应用一拨珠与写数一画图与摆物”。学生通过实物、操作、手势、画图、符号等多种直观方式，经历从数量抽象出数的过程，达成认识数的目标，发展学生的数感和符号意识。

（2）中段学生，在构建表象中应用序列化教学。小学三、四年级学生处于具体形象思维阶段，主要依靠事物的形象和表象进行思维。三、四年级的数学知识已经具有一定的抽象性。教师要以具体形象为支撑，在构建数学概念的表象中应用系列化教学，促进学生对数学概念的理解。如在学习“倍”时，可以立足具体形象，应用“圈一分一连一比一画”的序列性的教学，帮助学生在头脑中构建“倍”的表象，促进学生对“倍”的理解。圈一圈，知道6朵红花是2朵蓝花的3倍；分一分，知道12个圆圈是4个三角形的3倍；连一连，知道9个彩球是3个白球的3倍；比一比，发现前三组物体数量不同，但是二者之间的关系相同；画一画，用线段表示这个相同的关系。学生在序列化学习中，建立了3倍的表象，促进了他们对倍的理解。

二、小学数学序列性教学的实施策略

（3）高段学生，在数学推理中应用序列化教学。五、六年级学生的思维逐渐从具体形象思维向抽象逻在小学数学教学中，根据不同的学生、不同的内 辑思维发展。抽象逻辑思维是以概念、判断、推理的形式反映客观事物的本质特征和内在联系的思维[。在小学高段数学学习中，教师可结合数学推理开展序列化的学习，促进学生推理意识的发展。如在学习“钉子板上的多边形”时，教师可以应用序列化教学引导学生掌握多边形的面积与多边形边上钉子数和多边形内钉子数之间的关系：任务一，观察形内只有一颗钉子的图形的面积与边上钉子数的关系，通过合情推理得出“多边形的面积 Σ= Σ 边上钉子数 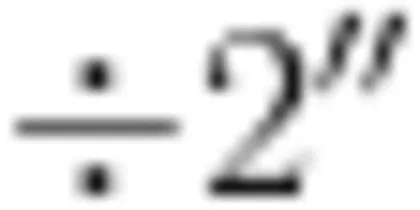；任务二，观察形内只有两颗钉子的图形的面积与边上钉子数和形内钉子数的关系，通过合情推理得出“多边形的面积 Σ= Σ 边上钉子数 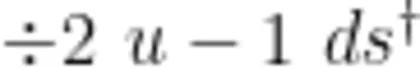；任务三，观察形内有不同数量钉子的图形的面积与边上钉子数和形内钉子数的关系，通过合情推理得出“多边形的面积 Σ= Σ 边上钉子数 ÷ 2 + 形内钉子数-1”。三次推理有序展开，使学生在循序渐进中探究出多边形的面积与边上钉子数和形内钉子数之间的关系，推理意识也得到了发展。

学生在小学数学学习中，依次经历序列化操作、序列化观察、序列化推理，形成序列化的思维，促进他们高阶思维的发展。

2.因“知”而序，促进内容序列化

小学数学教学内容分为“数与代数”“图形与几何”“统计与概率”和“综合与实践”四大领域。教师要依据不同领域的知识结构应用序列化教学，促进内容的序列化。

（1）立足计数单位，在数与运算中应用序列化教学。《义务教育数学课程标准（2022年版）》（下文称《2022版课程标准》）在“教学提示”中指出：“通过整数、小数、分数的运算，进一步感悟计数单位在运算中的作用，感悟运算的一致性。”[5]

在教学异分母分数加减时，教师可以立足计数单位应用序列化教学，引导学生感受计数单位在运算中的重要性，感悟加减运算的一致性。任务一，回顾同分母分数加减法：分数单位相同，分数单位个数相加减；任务二，探究异分母分数加减法：将不同的分数单位转化为相同的计数单位；任务三，比较整数、小数、分数加减运算：相同计数单位下计数单位个数的加减。在序列化教学中，学生不仅掌握了异分母分数加减法的计算方法，还沟通了整数、小数和分数加减运算之间的联系，体验计数单位对加减运算的作用，感悟整数、小数和分数加减运算的一致性。

（2）立足度量单位，在图形的认识与测量中应用序列化教学。在图形的认识与测量学习中，度量单位起着非常重要的作用，是学生对图形从直观感知到定量研究的转变。《2022版课程标准》在“课程内容”中指出：“图形的测量重点是确定图形的大小。基于度量单位理解图形长度、角度、周长、面积、体积。”7l如在学习线段的长度时，学生在具体的测量活动中感知“线段的长度就是其包含的长度单位的个数”；在学习面积时，学生通过单位正方形的拼摆，体会“图形的面积就是其包含的单位正方形的个数”；在学习角时，学生通过量角器量角理解“角的度数就是角所包含的单位角的个数”；学习体积时，学生通过拼摆单位小正方体理解“物体的体积就是其包含的单位小正方体的个数”。在序列学习活动中，学生逐步感悟度量单位在图形测量中的重要作用。