初中数与代数领域内容的结构化设计

教授、博士生导师，中国教育学会课程专业委员会常务理事，中国教育学会基础教育评价学会常务理事；义务教育数学课程标准研制组核心成员，全国中考数学评估组专家，全国高中数学学业质量监测评估组专家，北京师范大学教育质量协同创新中心数学首席专家；在Educationand InformationTechnologies，ComputersandEducation，Educational Studiesin Mathematics以及《教育学报》《教师教育研究》《教育科学研究》《数学教育学报》等国内外期刊发表论文100余篇，完成和在研项目20余项。

【关键词数与代数；结构化设计；运算；数学素养

数与代数领域内容是学生认知数量关系、探索数学规律、建立数学模型的基石。学习这些内容，有助于学生从数量的角度清晰准确地认识、理解和表达现实世界。良好的结构化教学设计不仅能帮助学生建立清晰的数学概念体系，还能提升他们的推理能力、抽象能力、运算能力和模型观念等数学核心素养。初中数与代数领域内容如何结构化呢？

一、数与代数各主题内部的结构化

1.“数与式”的结构化

“数与式”作为代数的基础内容，应帮助学生理解字母在表述代数式和代数式运算中的作用，掌握字母与数的类比关系，从而通过代数运算进行一般性推理。

对于“数”的内容，首要的是合理安排自然数、整数、分数、小数、有理数、实数等内容，使学生逐步理解数的性质及其运算法则。例如，学生要先在小学阶段学习自然数、整数、分数、小数及其基本运算等，到初中阶段再扩展至学习有理数、实数，进而理解数系扩充后的运算法则。在此过程中，教师可以利用数轴帮助学生直观认识数的连续性、比较数的大小;可以通过平方根概念引入无理数，引导学生理解实数体系的构成；等等。

对于“式”的内容，其层次性递进安排需以符号化思维为核心，构建从具体运算到抽象表达的认知框架。其教学可以从算术表达式入手，依托生活实例自然过渡到用字母表示数的基础代数式（单项式），帮助学生理解变量替代具体数值的意义；在此基础上扩展至多项式，让学生认识到代数式可以表示更复杂的数量关系；之后系统展开整式与分式的对比学习。在整式方面，通过单项式、多项式的加、减、乘运算（如合并同类项、分配律的应用等）强化代数变形规则；在分式方面，借助分母含字母的表达式，结合实际问题，强调分母非零的限制条件，辨析分式与整式的本质差异。

“数与式”的内容主线应为“有理数一实数一整式一分式”。这些内容通过数及运算、式及运算勾连起来，其教学应以数的运算规则为根基，逐步延伸至式的抽象表达。例如，在运算法则上，数的运算律可以自然迁移至式的运算。具体来说，有理数运算分配律的基本原理能延伸至整式乘法运算的展开过程中；分数的通分与约分逻辑与分式运算完全一致；等等。因此，数与式既存在具体与抽象的关系，又存在特殊与一般的关系。

2.“方程与不等式”的结构化

“方程与不等式"涉及一元一次方程、二元一次方程组、一元二次方程、不等式（组）及其解法等，它是代数知识体系的核心内容，是刻画数量关系的重要模型，其教学结构应呈现“纵向类比、横向推广"的立体化特征。

在纵向维度上，教师可以以“等式一不等式"为主线，先从等式性质（如等式两边同时加、减、乘相同的数，等式仍然成立）出发，引导学生掌握一元一次方程的解法，接着通过实际问题（如人教版教材中“销售中的盈亏"问题），引导学生理解方程是一种表达数量相等关系的数学模型，解题应聚焦于未知数取值的确定，然后通过类比等式引入不等式，引导学生探析等式和不等式在变形规则上的异同，揭示其共性与差异，最后以生活实例（如人教版教材中“消费方案选择"问题）凸显不等式在“范围分析"中的独特价值。这个过程能体现从确定性关系到不确定性关系的思维跃迁。

在横向维度上，这部分知识体系呈现“从单一到多元”的特征：一方面，从一元一次方程到二元一次方程组、三元一次方程组，强调利用代入、消元等方法研究多变量关系问题，深化学生对系统性建模的认知;另一方面，从单一不等式到不等式组，强调结合数轴法分析多约束条件下的解集关系，帮助学生掌握复杂问题的分层处理策略。这种结构既保持知识的内在一致性，又体现认知层次的提升。

“方程与不等式”知识的建构应以模型观念为纽带，通过方程与不等式的对比，形成“从等号到不等号”从单变量到多变量、从线性关系到非线性关系的结构化体系。这种设计方法有助于学生依托方程经验跨过不等式学习的门槛，通过差异性辨析提高数学思维的严谨性，最终实现从基础工具应用到复杂现实问题建模的能力跃迁。

3.“函数”的结构化

“函数"主要包括函数的概念、一次函数、二次函数和反比例函数。其结构化设计应主要以“变量关系”为核心，引导学生探索事物变化的规律，并通过层层递进的方式建立对函数的系统性认知。在内容结构上，三类初等函数均可遵循“概念一图象一性质一应用"的研究范式，如学习“二次函数”，可以先从典型生活情境中抽象出变量关系，接着用三种形式刻画函数的规律，然后借助图象分析函数的单调性、极值及变化趋势等，最后应用二次函数解决实际生活中的问题。在知识结构上，“函数"纵向衔接小学阶段变量关系的相关知识与高中阶段函数的形式化定义（如集合、映射等）；横向贯通“数与式”"方程”“不等式"等知识模块。具体而言，代数式是函数表达式的基础，坐标系提供图象分析工具，方程和不等式作为函数的特殊状态与函数具有内在联系。教师在教学中可以以数形结合为纽带将函数思想贯穿于方程、不等式的求解过程中，如通过函数图象交点求解方程、利用函数值域分析不等式解集等。

二、数与代数各主题之间的结构化

1.体现各主题内容之间纵向的逻辑关联实数、代数式、方程、不等式、函数具有纵向的逻辑关联。数是起点，实数通过字母表示数的符号抽象过程，并经过有限次的加、减、乘、除、乘方、开方等代数运算，可以转化为代数式；方程与不等式是用等号或不等号进行关系建模、连接代数式形成的；函数是用含有其他变量的代数式表示方程中一个变量形成的，它是动态关系抽象的工具。

2.通过内容结构的相似性强化认知结构

数与代数领域内容设计可以利用内容结构的相似性，强化认知过程中方法的一致性建构，这是结构化设计的一种体现。如有理数和实数的内容通常按照"定义一性质一运算一应用"的研究范式展开，这体现了内容的结构化。有理数的教学可以通过引入负数将自然数扩充到有理数，继而按照“有理数的概念一有理数的性质一有理数的运算一有理数的应用"学习路径进行。而实数的教学可以先复习有理数的学习路径，再类比这样的路径展开探究，让学生实现学习迁移。类似的，方程与不等式的常见研究范式是“概念一解法一应用”。研究函数，如一次函数和二次函数等结构相似的内容，通常遵循“概念一图象一性质一应用"的研究范式。研究范式的一致性不仅有利于凸显相关内容的内在结构，还有助于学生建立系统性思维，强化认知结构。

3.通过研究方法的引领建立知识结构

数与代数领域内容的结构化要关注知识之间的衔接和沟通，通过类比、归纳、推广、特殊化、转化等数学思想方法的引领，建立不同知识之间的关联。例如，算术中数的运算（如加法、乘法）可以类比迁移到代数中多项式的运算；算术中的等式性质可以推广到代数中方程的解法。又如，将无理方程通过平方运算转化为有理方程；将分式方程通过去分母转化为整式方程；将高次方程通过因式分解或换元法转化为低次方程；将多元方程通过代入法或消元法转化为一元方程。这种转化为构建结构化的方程知识体系提供了逻辑纽带。

三、教学建议

1.设计序列化问题，引发整体性思考

为了让学生建立结构化认知，教师应把握知识形成的关键点、知识之间的内在联系以及问题变式的发散点等，设计恰当且具有启发性的序列化问题，引发学生的整体性思考。以函数性质的教学为例，教师可以聚焦函数的性质有哪些、如何研究函数的性质等关键点及其关联，设计3个引导性问题，引发学生对函数本质的整体性思考与理解。问题1：什么是性质？性质是一类事物共有的特性。问题2：什么是函数的性质？现实世界中的某些变化会随着时间的推移而有增有减、有快有慢，有时达到最大值，有时处于最小值，这些现象反映到数学中，就是函数值随自变量的增加而增加或减少，以及函数值何时最大、何时最小的问题，这些问题对应函数的性质单调性、最大值、最小值。问题3：怎样研究函数的性质？教师可以引导学生利用函数的定义、图象、解析式展开研究，经历观察、实验、猜测、推理、交流、反思等数学活动，积累活动经验，发展数学思维，提高发现、提出、分析和解决问题的能力，培养独立思考、探究质疑、合作交流的学习习惯。

2.设计探究性任务，引导深度思考

在设计探究性任务时，教师应以引导学生深度思考为核心目标，通过精心设计的问题情境和任务结构，引导学生从表层知识学习转向深层次的理解与应用。首先，任务设计应基于学生的认知水平和兴趣点，选择贴近生活或具有挑战性的问题情境。例如，在“一元一次不等式"教学中，教师可以设计开放性问题：“某书店正在进行促销活动，购买图书可享受折扣。已知：购买金额满100元享受9折优惠；购买金额满200元享受8折优惠。请分析：在什么情况下一次性购买更划算？在什么情况下分两次购买更划算？是否存在一种能使实际支付金额最小的购买方式？如果有，请给出具体的购买策略。"作答这种问题，学生不仅需要运用方程及不等式知识深入分析问题，还需要结合实际情况优化方案。这种问题有利于培养学生的逻辑思维和问题解决能力。其次，任务设计应具有层次性，从简单到复杂逐步推进学生学习。最后，任务设计应体现一定自主性。教师应鼓励学生在探究过程中自主提出问题，并通过小组合作、实验验证、数据分析等方式寻找答案。例如，在探究“篮球抛物线运动”时，教师可以让学生实际测量篮球的投掷高度和距离，收集数据并尝试用二次函数建模，从而将数学知识与实际现象联系起来。此外，教师应注重任务的评价与反馈，通过学生自评、学生互评和教师评价相结合的方式，引导学生反思探究过程中的不足，提升思维深度和学习能力。

3.强化算理教学，突出代数推理

在数与代数领域内容的教学中，教师应强调算理与数学推理，因为这是提升学生数学核心素养的关键。算理教学应注重从具体到抽象的过渡，帮助学生理解算法背后的原理。例如，在“有理数的加减法"教学中，教师可以通过数轴直观演示运算过程，帮助学生理解负数加正数的算理。同时，教师应通过归纳法引导学生探索规律，如探究“三角形数”“环形点阵”等，理解相关计算公式或表达式的形成过程。在代数推理的训练中，教师应注重符号意识的培养和逻辑推理能力的提升。例如，在“数的整除性"教学中，教师可以借助逻辑论证问题，如“证明四位数 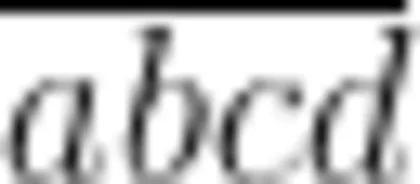能被4整除的充要条件是其末两位数 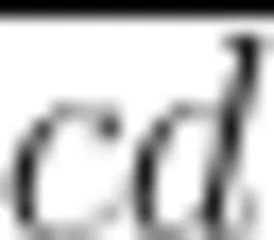能被4整除"等，培养学生的符号意识和推理能力；在“一元二次方程"教学中，教师可以引导学生通过配方法推导求根公式，体会代数推理的普遍性；在“函数"教学中，教师可以引导学生分析函数图象的变化规律，发展几何直观和推理能力；等等。

数与代数领域内容的结构化设计对数学学习至关重要，教师可以通过合理组织知识内容，构建各部分内容之间的逻辑联系，并在教学中通过设计序列化问题、探索性任务以及强化推理训练等教学手段，帮助学生形成完整的数学认知体系，增强数学核心素养，使其具备解决复杂问题的能力。

（姜惠敏系新疆石河子大学理学院副教授，黄建系四川省汶川中学校高级教师、北京师范大学访问学者）

文字编辑刘佳