数学课程美育：逻辑与形式的和谐交响

李如密，课程与教学研究所所长、教授、教育学博士，课程与教学论专业博士生导师，兼任中国教育学会教育学分会常务理事、中国教育学会教育学分会教学论专业委员会副理事长、中国高等教育学会学习科学分会副理事长、全国现代教学艺术研究会副理事长，主要从事教学理论研究，著有《教学艺术论》《教学风格论》《现代教学理论研究》《教学美的价值及其创造》《儒家教育理论及其现代价值》《孔子教学艺术研究》等，在《教育研究》《课程·教材·教法》《中国教育学刊》等期刊发表论文400余篇。

数学美是一种独特而深刻的美，它源于数学本身的严谨性、逻辑性和抽象性。著名哲学家、数学家罗素（Russell）曾言：“正确看待数学，它不仅拥有真理，而且拥有至高无上的美能够达到只有最伟大艺术才能表现出来的严格的完美。"《义务教育数学课程标准（2022年版）》多次强调数学美的价值导向，为数学课程美育明确了价值定位与实践追求。探讨数学美的表现，以及数学课程美育的实现途径，是一件重要而有趣的事。

一、数学美：数学课程美育的丰富资源

数学美兼具数学特性和美学属性，是课程美育的重要资源。数学美的表现主要有以下几个方面。

1.简洁美

数学家总是追求用最简洁的语言、最少的符号表达最丰富的数学内容。这种简洁性不仅使数学易于理解和传播，还赋予数学独特的美感，给人带来视觉上的愉悦和思维上的震撼。数学的简洁美主要体现在数学的符号表达、公式构建及逻辑架构中。例如，勾股定理"如果直角三角形的两条直角边长分别为 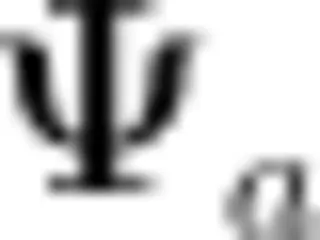和b，斜边长为 c ，那么 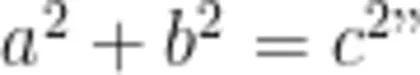，用简单的等式揭示了直角三角形三边的关系“两直角边的平方和等于斜边的平方”；欧拉公式 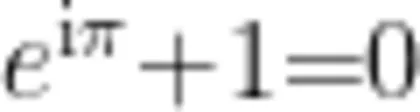是数学中揭示复数指数函数与三角函数关系的核心等式，它用三个变量统一了多面体的拓扑性质，被誉为“数学界的诗篇”；等等。

2.和谐美

经典的美学观点认为美是和谐的。数学美的本质在于其内部的和谐与统一，是数学对自然规律和谐、统一与有序的反映。这是因为数学公式、定理和概念之间往往存在紧密的内在逻辑关系，这种和谐性使数学成为一个有序、统一的整体。数学和谐美的突出表现是对称性，它是和谐的结构化表现，是数学美的重要特征之一。对称美在数学中广泛存在，体现在几何图形的对称性、代数表达式的对称性等方面。几何图形的对称性方面，等腰三角形、长方形、圆等几何图形都展现出完美的对称美。代数表达式的对称性方面，二次函数图象（抛物线）呈现轴对称特征；三角函数中正弦函数和余弦函数的图象也呈现出对称性。“匀称性”也可以看成数学和谐美的一个特征，黄金分割就是一个典型的例子，如根据此原理配比长和宽所构成的长方形给人以“匀称美”的感觉，因此黄金分割比（0.618）被誉为“人间最美妙的比例”。

3.奇异美

英国著名思想家培根（FrancisBacon）曾说：“美在于独特而令人奇异，奇异与和谐是对立的统一。”数学中存在着许多奇异而美妙的现象，这些现象往往超出人们的日常经验，展现出数学独特的魅力。如，在分形几何中，人们可以看到一个图形在不同尺度下呈现出相似的结构，这种自相似性使分形图形具有一种奇异的美感。徐本顺教授指出：数学解题方法的奇异性与文学中那种奇峰突起的“神来之笔”相似，令人体会到一种奇特新颖之美感。这种奇异美使数学充满神秘感。对数学奇异美的追求有助于学术创新，数学家正是通过不解的探索和研究，才不断发现新的数学现象，提出新的数学理论和方法。如费马大定理的证明历经300多年，最终由安德鲁·怀尔斯通过椭圆曲线和模形式理论完成；黎曼猜想是数论中最著名的未解决问题之一，它激发无数数学家进行创造性研究。

4.深邃美

数学的深邃美首先表现在它的抽象性上，这是数学美的特殊性所在。数学通过抽象化揭示普遍规律，如群论通过抽象的代数结构研究对称性和变换，被广泛应用于物理学、化学和密码学领域；范畴论是高度抽象的数学分支，试图统一数学中的各种结构。

数学的深邃美还体现在其含蓄性上。许多数学定理和公式蕴含着深刻的思想，需要人们通过深入思考和领悟，发现其内在的美。这种含蓄美使数学具有一种深沉和内敛的美感。如斐波那契数列是一个从0和1开始，之后的每一个数字都是前两个数字之和的数列。斐波那契数列的美不仅仅在于其简单的递推关系，更在于其所蕴含的深刻数学原理能反映诸多自然现象，形成一种和谐之美。

二、数学融美教学：数学课程美育的重要途径

1.开发数学课程的“融美点”，发现数学之美

数学教材是数学知识技能和思想方法的载体，教师应深入挖掘数学教材中的“融美点”。如教学“小数除法"时，教师可以引导学生在理解小数除法的算理依据是“商不变性质”算法核心是“转化成整数除法"的过程中，感受数学知识结构一体化，体会数学知识的统一美;在认识循环小数、掌握循环节的简便记法的活动中，感受数学符号的简洁美；在用计算器计算、观察计算结果、发现规律和利用规律续写算式的活动中，感受数字排列规律的奇异美；在探索数字黑洞的游戏中，感受数学运算陷人循环的奇妙现象，体会数学的奇异美。聚焦这些数学教材“融美点”，教师可以更有针对性地落实数学课程美育，成为学生数学审美学习的引导者，引导学生发现并欣赏数学之美。

2.将抽象的数学知识具象化，丰富审美感知

教师通过创设课程美育情境将抽象的数学知识转化为具象形态，可以更好地丰富学生的审美感知。具象化的策略有四种：其一，语言叙述故事，如在讲解数学公式、定理、定义时，教师可以通过讲述故事的形式描述数学家发现数学规律的情景，让学生充分体验数学的简洁美及抽象美；其二，动画展演变化，如在轴对称图形的教学中，教师可以通过设计艺术性动画，生动演示图形的对称变化，让学生更直观地感受轴对称图形的和谐美；其三，真实生活例示，如在教学某个抽象的数学原理时，教师可以列举生活实例，让学生通过现实印证发现数学的奇异美与深邃美；其四，创设环境浸润，如教师在教室里布置数学展板、几何艺术装置等时，可以将分形图案、黄金分割比等融入其中，打造沉浸式数学美育空间。以上具象化策略，可以有效克服数学知识抽象性所带来的学生学习障碍。

3.调动数学审美活动的参与感，激活审美体验

教师要组织多样化的数学审美活动，让学生积极参与其中，获得相应的审美体验。其一，游戏活动。教师可以开发数学解谜闯关游戏，通过“玩数学”吸引学生参与，让他们从中体验数学学习的乐趣。其二，图案探究活动。教师可以在数学方程中嵌入蝴蝶曲线、心形线、玫瑰线等优美的图案，让学生体会数学的神奇与妙趣。其三，剪纸创作活动。教师可以让学生用剪纸方式创作具有几何特点的图形，提升其数学审美想象力。其四，作品展览活动。教师可以通过组织数学主题展，展示学生的数学作品和成果，如数学模型、创意设计等，增强学生的成就感。其五，文化交流活动。有条件的学校和教师可以组织学生开展中外数学文化交流活动，深化学生对不同数学文化的了解，培养他们的文化修养和国际视野。学生在数学审美活动中积极参与数学审美学习，会留下深刻的具身审美体验。

4.适当提升与艺术形式的融合度，增添审美趣味

数学课程与艺术形式融合会产生奇妙的效果。首先，融合诗歌，给数学课程增添诗意。李尚志教授常常用诗描述数学，如用“东升西落照苍穹，影短影长角不同。昼夜循环潮起伏，冬春更替草枯荣"描述三角函数等，他把诗歌运用到数学教学中，展示数学的本质，让数学既美又好玩，让学生爱上数学。其次，融合音乐，给数学课程美化形象，如教师可以结合音乐节奏设计分数计算活动，将音符时值与分数运算结合，实现数理逻辑与韵律美的共振。再次，融合戏剧，增强数学课程吸引力，如教师可以组织《数学星空下的追光者一一陈景润》角色扮演活动，让学生通过剧本演绎感受数学家对数学的热爱和对真理的执着追求。最后，融合其他艺术形式，实现数学课程趣味化，如教师可以引导学生用折纸艺术探索几何图形对称性，通过莫比乌斯环剪纸操作理解拓扑变换等。跨学科融合的教学方式能使学生在轻松愉快的氛围中学习数学知识，达到数学课程美育的目的。

5.聚焦学生数学审美创造力，发展审美思维与理性精神

教师要鼓励学生在数学课程中进行审美学习与创造，发展审美思维与理性精神。其一，努力寻求简洁新颖的“最优解”。在数学解题过程中，教师应引导学生运用创造性思维，对比不同解题路径，寻求体现简洁美的“最优解”。教师也可以设计“公式变形挑战赛”，引导学生比较等差数列通项公式的多种推导路径，评选“最优解”并分析其简洁性价值。其二，培育数学与审美结合的“统合眼光”。如，在绘制轴对称图形的过程中，教师应鼓励学生运用美的眼光欣赏图形的变化所创造出来的美感，逐步发展学生的空间观念和对几何图形的审美鉴赏能力。再如，教师可以设计“最优校园快递柜布局"项目，要求学生综合考虑取件效率、空间利用率和视觉协调性等因素进行设计。学生需要用几何知识设计柜体组合方案，用概率模型模拟人流动线，最终通过3D建模呈现兼具功能性与美学价值的设计方案。其三，发展深邃含蓄的“理性精神”。如在命题证明教学中，教师可以设计“反证法剧场”活动，引导学生通过辩论体会数学推理的排他性美感；展示欧几里得《几何原本》公理体系演化史，引导学生通过与传统几何体系对比，体会非欧几何的突破性，感悟逻辑体系的动态发展美。学生数学审美创造力的发展，必将助力他们攀登数学理论与实践的高峰。

参考文献：

[1]Russell B，Rempel R A，Brink A，et al.TheCollected Papers of Bertrand Russell：Volume12[M].London：Routledge，1985：86.

[2]徐本顺，殷启正.数学中的美学方法（第2版）[M].大连：大连理工大学出版社，2016.61.

[3]李玲玲.融美数学：探寻小学数学课堂新境[M].重庆：西南大学出版社，2024.76.

文字编辑孙爱蓉