核心素养导向下中考数学命题特点探析
作者: 沈占立 郑轶群沈占立,正高级教师、湖北省特级教师、湖北名师、湖北名师工作室主持人,曾获湖北省骨干教师、教改先进个人及武汉市百优班主任等称号,执教的课例获评“一师一优课”部级优课奖项,在省级及以上刊物发表中学数学教学类文章近200篇,著有《粉笔留痕》引领卓越》。近期,工作室深入研究新中考数学备考策略,旨在为复习教学提供借鉴。
核心素养导向下,中考数学命题关注数学本质与通性通法,注重创设真实情境,提出有意义的问题,综合考查“四基”“四能”和核心素养,并适当提高应用性、探究性、综合性试题比例,以相对全面地考查义务教育数学课程学业质量。通过对全国各地中考数学试卷的综合研究,我们发现一系列能体现教育改革新理念、助推学生综合素质提升的高质量试题。笔者结合具体例题探析当前中考数学命题特点。
一、融入文化素材,发挥立德树人教育功能
当前,多地中考改革方案明确指出,要积极培育和践行社会主义核心价值观,大力弘扬中华优秀传统文化、革命文化和社会主义先进文化。在此背景下,中考数学命题越来越关注文化元素,通过在试题中融入“三种文化"或数学文化素材,提高学生的文化素养和学习兴趣。
例如,2024年武汉市中考数学试卷第1题让学生从“遇、见、美、好"中选择具有对称性的汉字,除了检验学生对轴对称图形特征的理解与应用水平,还蕴含着深层的教育意图,即通过选取具有深厚文化底蕴的汉字作为考查载体,在展现汉字结构美的同时,体现数学在形式与逻辑上的严谨美。这种命题方式有利于引领学科教学落实“三种文化"的渗透。
又如,2024年湖北省中考数学试卷第7题。
我国古代数学著作《九章算术》中记载了一个关于方程组的问题:“今有牛五、羊二,直金十两。牛二、羊五,直金八两。问牛羊各直金几何?”译文:“今有牛5头…各值金多少?”若设牛每头值金 x 两,羊每头值金 y 两,则可列方程组是( )。
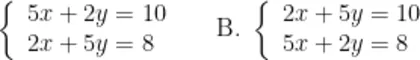 福
福 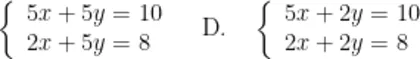
这道题以《九章算术》为背景,考查学生列二元一次方程组解决问题的能力。这种将数学知识与数学文化相结合的命题方式丰富了数学教育的内涵,有助于学生增强民族自豪感,坚定文化自信。
通过对同类题型的综合分析,笔者提出如下复习备考策略。首先,教师要深入了解中外数学史,包括重要数学家的贡献、数学定理的发现过程等内容,据此设计专题复习,将数学文化渗透与解题策略总结相结合,并通过观看数学文化纪录片、虚拟参观数学博物馆等教学形式,丰富学生的学习体验。其次,教师要关注与数学相关的科技革新、数据分析等方面的时事新闻,针对性设计应用题,引导学生提取、分析其中的数学问题,增强理论联系实际的能力。
二、设置真实情境,考查解决问题能力
创设真实的问题情境、突出解决问题能力的考查已成为当前中考数学命题的重要趋势。这样命题有利于考查学生灵活运用数学知识创造性解决复杂实际问题的能力,引领教学注重学生应用意识与创新思维的培养。笔者以2024年成都市中考数学试卷第15题为例分析。
2024年成都世界园艺博览会以“公园城市美好人居”为主题…向世界人民传递绿色发展理念和诗意栖居的美好生活场景某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、亲子互动漫游线、园艺小清新线)中选择一条。现随机选取部分员工进行了“线路选择意愿”的摸底调查,并根据调查结果绘制如下统计图表。
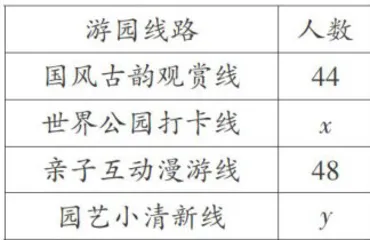
根据图表信息,解答下列问题:
(1)本次调查的员工共有 人,表中 x 的值为;(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数。
试题具有真实性和时代感,能激发学生解题的兴趣;涵盖多个统计图表的知识点,能充分考查学生的数据解读与分析能力、问题解决能力、综合应用能力。
对此类问题,复习备考可以采取以下策略。首先,教师可以在复习中引人结合社会公益、环境保护等实际情境设计的数学题,帮助学生积累素材,理解准确解题对现实生活的意义。其次,教师要引导学生关注时事热点与日常生活,理解事物现象背后的数学原理,提升在真实情境中识别数学问题和应用数学知识解决问题的能力。再次,教师要注重解题步骤的归纳,引导学生明确问题解决的一般流程,如审题、分析、建模、求解、验证等。最后,教师要引导学生在每次练习后反思解题思路、总结解题技巧,以便在遇到相似问题时迅速找到解决方案。
三、强化实践导向,考查动手能力
注重试题的操作性、突出动手能力的考查是当前基础教育考试命题的发展趋势。在此背景下,中考数学命题着力强化实践导向,引导学生通过操作解决问题,考查他们的知识运用能力与实践能力。笔者以2024年广东省中考数学试卷第21题为例分析。
综合与实践【主题】滤纸与漏斗【素材】如图21-1所示:
① 一张直径为 1 0 c m 的圆形滤纸;
② 一只漏斗口直径与母线均为 7 c m 的圆锥形过滤漏斗。
【实践操作】
步骤1:取一张滤纸步骤2:按如图21-2所示步骤折叠好滤纸步骤3:将其中一层撑开,围成圆锥形
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:hbjx20250520.pd原版全文
步骤4:将围成圆锥形的滤纸放入如图21-1所示漏斗中
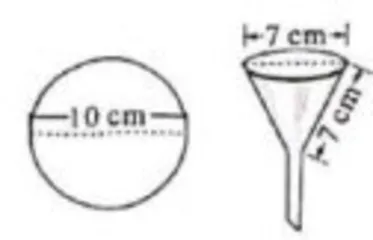
图21-2
【实践探索】
(1)滤纸能否紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明。
(2)当滤纸紧贴漏斗内壁时,求滤纸围成的圆锥形的体积。(结果保留 π )
试题聚焦“综合与实践”设计,引导学生折叠滤纸、围圆锥等,不但能综合考查学生数学知识的掌握情况,而且能检验学生动手能力的发展情况。特别是实践探索板块,学生需要运用圆锥侧面展开图与扇形弧长公式,判断滤纸展开后的弧长是否等于漏斗底面周长;通过相似三角形求圆锥的高,而后代入圆锥体积公式计算。这能有效检验学生提取操作经验解决问题的能力。
针对考查动手能力的实践导向试题,笔者概括以下几点复习备考策略:一是增加操作类练习,如几何图形的折叠、拼接、测量,几何画板的动态演示等,让学生在操作中掌握知识技能,积累活动经验;二是探索模拟实验操作题,如涉及物理学、化学等实验操作的数学题可以通过模拟实验方式复习,让学生熟悉实验步骤和注意事项,提炼解题策略。此外,教师要注重复习材料的多样化,为学生创造更多的动手操作机会。
四、注重问题结构,考查知识体系
注重试题的结构性、突出知识体系的考查已成为基础教育考试命题的重要导向。这一命题导向强调试题设计应层次分明、逻辑严密,全面检验学生对知识体系的掌握程度和综合运用知识的能力。笔者以2024年广州市中考数学试卷第24题为例分析。
如图,在菱形 A B C D 中, 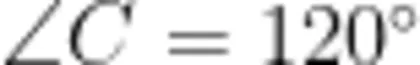 ,点 E 在射线BC上运动(不与点
,点 E 在射线BC上运动(不与点 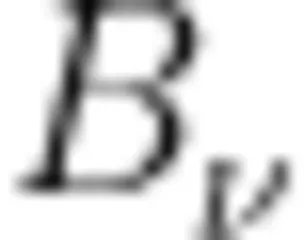 点 C 重合), Δ A E B 关于 A E 的轴对称图形为
点 C 重合), Δ A E B 关于 A E 的轴对称图形为 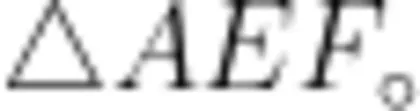
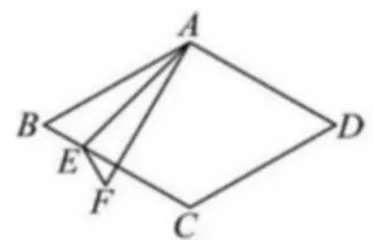
(1)当 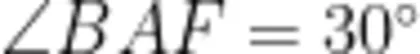 时,试判断线段 A F 和线段 A D 的数量关系和位置关系,并说明理由。
时,试判断线段 A F 和线段 A D 的数量关系和位置关系,并说明理由。
(2)若 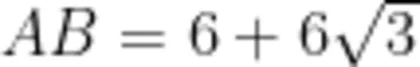 , ⨀ o 为 Δ A E F 的外接圆,设 ⨀ o 的半径为
, ⨀ o 为 Δ A E F 的外接圆,设 ⨀ o 的半径为 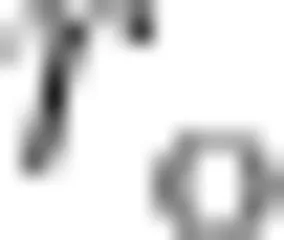
① 求 r 的取值范围。
② 连接 F D ,直线 F D 能否与 ⨀ o 相切?如果能,求 B E 的长度;如果不能,请说明理由。
试题从基础性问题开始,先要求判断线段 A F 和线段 A D 的数量和位置关系,这涉及菱形的基本性质、轴对称图形的性质及角度计算等基础知识。然后,试题难度逐渐提高,要求求解外接圆半径r的取值范围,这需要深入理解圆的性质、三角形的外接圆以及不等式的相关知识。最后,试题提出一个探究性问题(第 ② 小题),这需要综合应用直线与圆的位置关系、切线长定理及前述知识点解决。试题将这些知识点串联起来,形成一个完整的知识系统,凸显了对学生逻辑推理、运算能力、创新意识等的培养。
对这种类型的试题,笔者提出如下复习备考策略:一是通过综合练习系统梳理知识点,引导学生形成清晰的知识框架,加深理解和记忆;二是实施分层复习,根据试题难度和知识深度分层设置复习目标,引导学生逐步提升解题能力。
五、增强综合性,考查探究能力
突出考查探究能力的试题必然具有较强的综合性。综合性试题往往融合多个知识点且情境复杂。笔者以2024年上海市中考数学第24题为例分析。
平面直角坐标系中,已知抛物线 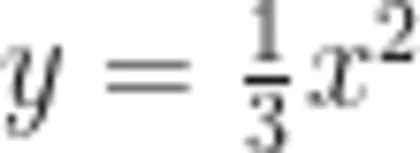 ,将其平移后得到的新抛物线经过点
,将其平移后得到的新抛物线经过点 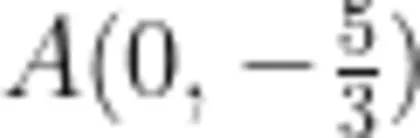 和点 B ( 5 , 0 ) 。
和点 B ( 5 , 0 ) 。
(1)求平移后新抛物线的表达式。
(2)直线 x = m ( m > 0 与新抛物线交于点 P , 与原抛物线交于点 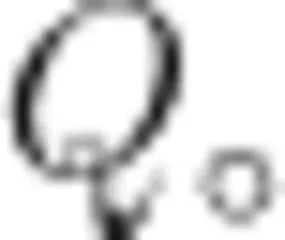
① 若PQ小于3,求 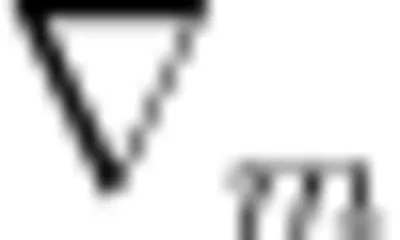 的取值范围。
的取值范围。
② 点 P 在原抛物线上的对应点为 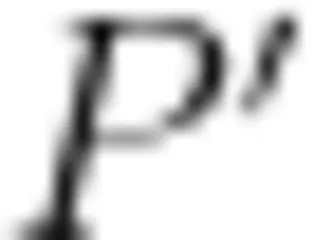 ,如果四边形PBPQ有一组对边平行,求点 P 的坐标。
,如果四边形PBPQ有一组对边平行,求点 P 的坐标。
试题融合抛物线平移、解析式求解、直线与抛物线交点问题、不等式求解以及几何图形的性质(如平行四边形的判定)等知识点,要求学生具备扎实的基础知识和综合运用知识的能力。第一问要求通过给定的点 A , B 求解平移后的抛物线解析式,学生需要深刻理解二次函数的平移性质,并通过代数运算求解。第二问提升难度,要求探究直线 x = m 与两条抛物线相交于点P,Q所形成的问题,包括两点间的距离以及由这些点构成的四边形PBPQ的几何特性(如平行边的存在性),学生需要具备较强的逻辑推理能力和问题解决能力才能作答。总之,本题具有挑战性,能综合考查学生数学核心素养的发展情况。
针对中考数学综合性试题的复习备考,笔者提出以下两点建议。其一,教师要分类筛选综合性强的、兼具深度与广度的复习题。这些题应体现不同主题或领域知识点之间的交叉融合,以及数学思想方法的综合运用,以助力学生提高解题的灵活性与探究能力。其二,教师应设置需要团队协作探究的综合题,让学生小组合作探讨研究方法,通过交流、碰撞解题思路,形成更加完善、高效的解题策略和模型,以便在遇到类似问题时能快速调用相应策略和模型解题。
(作者单位:武汉市光谷实验中学)
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:hbjx20250520.pd原版全文