初中数学“A形”相似专题复习核心策略

组织典型的复习内容是专题复习取得良好成效的基础和前提。专题复习不可能面面俱到，教师应基于课程标准和教材中的核心内容整体规划复习内容，由面到线、由线到点地确定内容主题。教师要注意所选素材的代表性和研究价值，不能孤立地选择高频考题，因为专题复习素材应适用于数学通性通法的研究和提炼，具有较强的延展性和探究性。基于此，笔者先从若干核心知识板块中选择相似三角形这个“面”，再从这个“面"中选取相似基本图形这条“线”，最后确定“A形”相似基本图形这个“点"作为相似三角形专题复习的切人点和落脚点，使之贯穿复习教学全过程。同时，“A形”相似基本图形是多地中考数学命题的重要内容，它可以与方程、函数等知识融合，有助于培养学生的分析与综合、比较与类比、归纳与演绎等思维方法。

一、架构复习路径，形成结构化认知

知识的简单再现只能起到巩固记忆的作用，而充分的纵向变式和横向关联可以实现认知的结构化，提高复习效益。

1.“A形”呈现

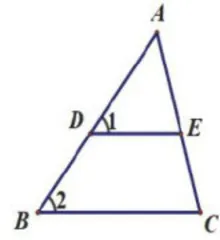
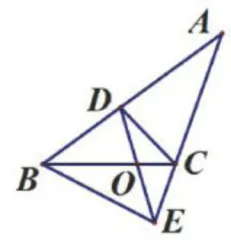
基于学生已有认知，笔者引导他们画出“A形"相似基本图形，并写出相应的条件和结论。学生画出如图1所示图形，并给出条件"点 D ， E 分别在 Δ A B C 的

边 A B ， A C 上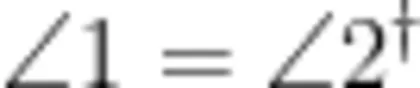， ”和结论“ ①Δ A D E ～ Δ A B C .

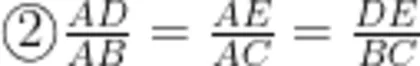；O

2.纵向变式

在学生巩固原形的基础上，笔者通过问题串逐步引导学生依次梳理出多种“A形”相似变式问题，以便后续总结提炼。

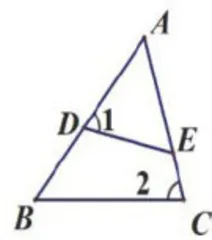
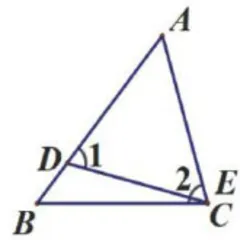
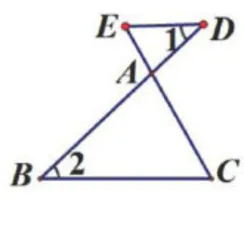
笔者先提问：如图2，改变图1中∠2的位置，你又能得出什么结论？学生回答： Δ A D E ～ Δ A C B 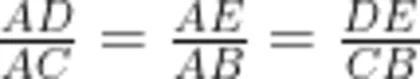。由此，“斜A形"相似问题被引入。

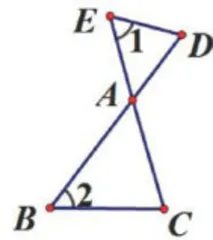
接着，笔者引导学生把图2特殊化，设计变式图形。学生得出如图3所示的“子母形”变式图形。在此基础上，学生把图3中 ∠ 1 和∠2特殊化，得出如图4所示的“射影形”变式图形。

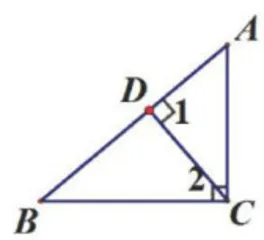
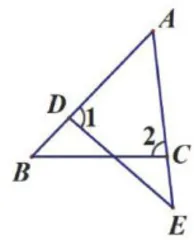
然后，笔者改变变式方向，先引导学生将图2中的线段 D E 向下平移至点 E 在线段 A C 的延长线上，得到如图5所示的“燕尾形”变式图形，然后引导学生将图1中的线段 D E 向上平移至点 点 E 分别在线段 B A C A 的延长线上，得到如图6所示的"X形”变式图形。学生类比“X形"变式的过程，基于图2又得出如图7所示的“8字形”变式图形。

为巩固上述变式问题，笔者综合“斜A形、8字形、燕尾形"设计如下题目。如图8所示，点 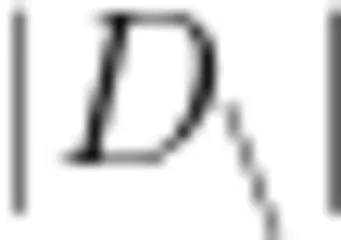点 C 分别在 Δ A B E 的边 A B ， A E 上， ∠ D B C = ∠ C E D ，求证：

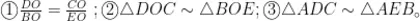
学生通过模型识别、转化和应用解决了这个问题，强化了解题技能。

最后，为拓展学生思维，笔者引导他们在图1和图6中加一条过点 A 的直线，使之与线段BC和 D E 相交，得出如图9和图10所示的“双A形”和“双X形"变式图形（也称“线束图”）。

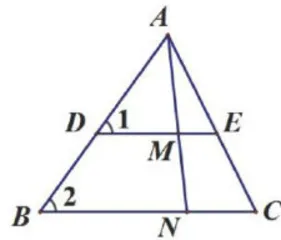
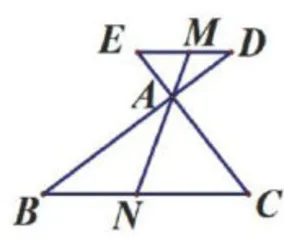
上述各类变式图形主要通过改变“A形”个别线段的位置、特殊化处理、增加线段使“A形"异化等方式得出。这些变式图形与"A形"整体构成三角形相似模型，实现了以点串线的复习素材组织方式。笔者在课堂上引导学生分析这些变式图形的差异性和相似性，使学生形成以下理解。其差异性体现于位置关系变化导致的相似三角形元素对应关系的不同，从而获得不同的线段比例关系。其相似性体现于以下两个方面：一是由图2到图3、图4的变化体现从一般到特殊的关系，由图1、图6到图9、图10的变化可理解为从简单的“A形"图、“X形"图进阶到复杂的"线束图”；二是图1、图6、图9、图10可归纳为平行截线相似模型，图2、图3、图4、图5、图7可归纳为斜截线相似模型。经过总结，学生认识到这些基本图形都以存在相似三角形为核心特征，并且它们之间可以相互转化、有机结合。

求异过程使“A形”相似模型变得丰满，求同过程使学生理解更加深刻，形成结构化认知，两个环节共同提高了学生复习的效率。

3.横向关联

知识发散不仅需要纵向演绎，还需要横向关联，以达成各知识板块的融合。首先，笔者横向关联三角形属性，引导学生将“A形”相似系列模型与直角三角形、等腰三角形关联，实现特殊三角形性质与相似问题的融合。其次，笔者横向关联平行线属性，引导学生将“A形”“X形”相似模型及其变式中的平行线特质与平行四边形（含菱形、矩形、正方形）、梯形关联。再次，笔者横向关联角度关系，引导学生基于“A形"相似模型及其变式中含有的等角关系，将这类问题与直线形及圆中的等角关系问题关联。最后，笔者横向关联运算，引导学生将相似三角形中的比例式证明或计算与解三角形、方程、函数问题关联。

学生深入理解“A形”相似模型及其变式问题后，笔者呈现两道中考题（题目内容略）作为拓展练习，一道题是2024年宁夏中考数学试卷第21题，另一道题是2011年武汉中考数学试卷第24题。这些题目具有较强的综合性和研究价值且解法较多，能让复习走向深入。

二、聚焦方法提炼，强化数学思维

解题方法的提炼是专题复习的重要目标和任务，有助于学生提升数学思维。解题方法需要借助具体的解题过程提炼，也需要专门研究。因此，笔者单独设置一个课时，依托以下几道典型题，引导学生从方法形成、异同比较、层次归类三个层面提炼解法。

1.方法形成分析

笔者先引导学生用多种方法作答如下题目。

如图11所示，在 Δ A B C 中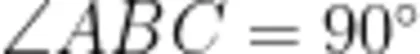， ， A B = B C ， M 是线段 B C 上一点，连接 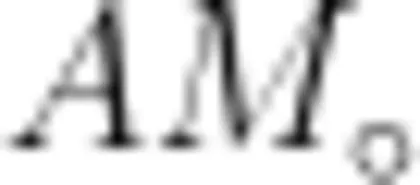过点 B 作 B P ⊥ A M ， P 为垂足，连接 C P 并延长，交线段 A B 于点 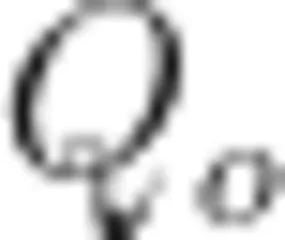求证：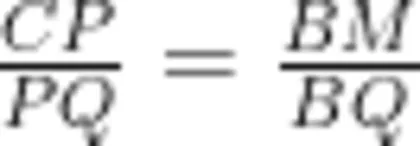

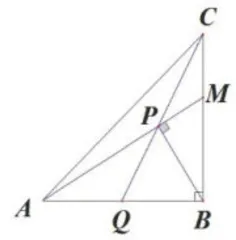
学生汇报交流后，笔者梳理出如下5种解法：解法1是作 C H / / A B 交 B P 的延长线于点 H ， 构造“X形”相似图形；解法2是延长 A B 至点 D ，使 B D / = B M ，连接c D ，构造“A形”相似图形；解法3是过点 Q 作QE//P B 交 C B 延长线于点 E ， 构造“A形”相似图形；解法4是作 P H ⊥ A B 于点 H ， 设 ∠ Q C B = α ， ∠ B A P = β . ，借助“A形”相似图形和三角函数证明；解法5是如图12所示，分别以直线 A B ， B C 为 x 轴、 y 轴，以点 B 为原点建立平面直角坐标系，设 A B = B C = 1 ， B Q = a ， B M = b ，作P G ⊥ A B 于点 G ， 借助"A形”相似图形和坐标系证明。