初中旋转变换结构化复习策略探析

为破解传统复习知识巩固碎片化、题型练习机械化、反馈指导笼统化的问题，本文聚焦知识联结、方法迁移、策略优化，探析旋转变换的结构化复习策略。

一、知识结构化：构建三层认知体系

1.生活化切入，夯实概念根基

把握旋转三要素是理解旋转变换的关键点，笔者借助生活素材巩固学生对旋转三要素的认识，夯实基本概念。对旋转中心，笔者通过门开合过程中门轴这个固定点等生活实例，强化学生对“不动点”作用的认识。对旋转方向，笔者借助钟表指针运动轨迹等，向学生强调顺时针方向与逆时针方向的规范定义。对旋转角度，笔者利用动态模型，如正方形纸片绕中心点旋转 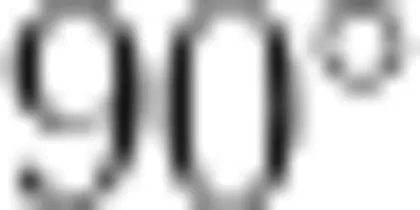后与原来的图形重合、钟表走动15分钟对应分针顺时针旋转 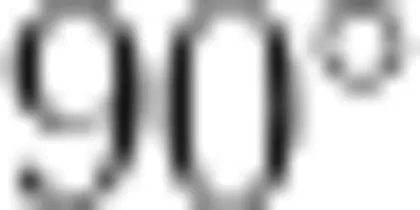等，深化学生对旋转角度与图形位置动态关联的认识。在此基础上，笔者结合实例引导学生从几何直观、代数表达和三角函数值三重视角理解和描述旋转角。

2.系统性联结，构建知识网络

为帮助学生构建旋转性质“推理链”，笔者从旋转三要素出发，引导学生发现旋转变换与其他几何知识的内在联系，构建知识网络。首先，基于“找对应点 对应点到旋转中心等距 对应边长度守恒 旋转角相等 图形全等”的递推关系，建立证明框架；其次，通过平移、轴对称等变换与旋转变换的对比，凸显旋转“绕点保距"的独特性；最后，结合正三角形绕中心点旋转 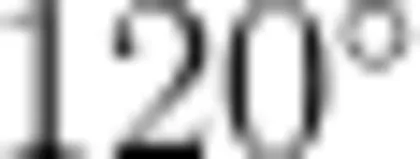后“自重合”、圆绕圆心旋转任意角度后“恒重合"等案例，深人理解全等变换。

在跨模块知识融合方面，笔者先将旋转与对称结合，引导学生分析图形旋转 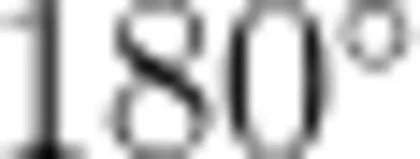与中心对称的等价性，然后将旋转与相似联动，引导学生探究旋转缩放复合变换下相似图形的构造（如三角形相似中的“一旋转二相似"模型），最后将旋转与对称、函数图象融合，通过平面直角坐标系中点旋转的坐标变换，向学生渗透函数图象旋转规律，如抛物线关于 x 轴、y 轴对称或绕坐标系中某个点旋转 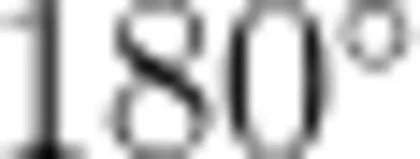时，只要将顶点按要求对称或旋转，再结合新的开口方向（开口大小不变），就可以直接得到新图象的解析式。

3.深层次拓展，强化数学本质

笔者从三个方面拓展学生的思维深度：一是运动观的培养，把旋转视为图形在平面内的位置变化运动，理解其“保距、保角"特性；二是不变性的挖掘，分析旋转过程中线段长度、角度大小、图形面积的不变性；三是对称美的感悟，基于敦煌藻井纹样、雪花晶体等艺术图案，赏析旋转变换的对称美。

二、题型结构化：实施四阶复习策略

1.基础操作题：三步规范作图

基础操作题的错误往往集中于选错旋转中心，如在平行四边形绕对角线交点旋转的情况下，部分学生错误地把图形顶点作为旋转中心。对此，笔者总结“定中心、标方向、抓关键点”三步规范作图法，即先根据题目描述或图形特征确定旋转中心（如平行四边形对角线交点），然后用箭头标明旋转方向，若题目未说明则需讨论两种可能，最后连接旋转后的各顶点，并用圆规确保对应点到旋转中心等距。

2.综合推理题：四步破解难题

教师可以引导学生通过“模型识别一方法提炼—结论梳理一体系建构"四个步骤破解难题。以“手拉手模型构造技巧"复习教学为例。课堂上，笔者呈现2024年深圳某区期末数学试题。

（1）如图1，已知， Δ A B C 和△ECD是等边三角形，点 B ， C ， D 在同一直线上，连接 B E ， 和边 A C 交于点 G 连接 A D 和 B E 交于点 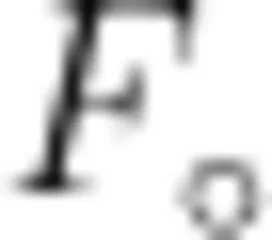求证：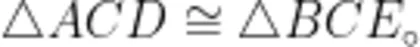

（2）在（1）的条件下，如图2，将 Δ E C D 绕点 C 顺时针旋转一定的角度 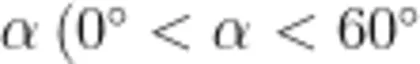），连接CF。 ①∠ A F B = ·② 猜想线段 C F ， A F 和 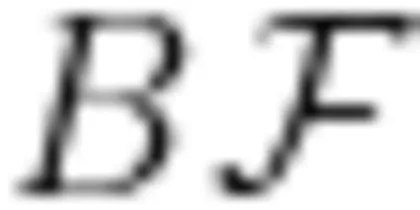的数量关系，并证明。（如果证明需要用到 ① 的结论，可以直接使用，无需再次证明。）

（3）如图3，在 Δ A B C 中， A B = A C ，过 Δ A B C 外一点 D ，作 ∠ A D B = ∠ A C B ， B D 和边 A C 交于点 F ， 连接 C D ，过点 A 作 A E ⊥ B F ， ，垂足为点 E ，若 C D = 3 B D = 9 ， A D = 7 ，请直接写出 的值。

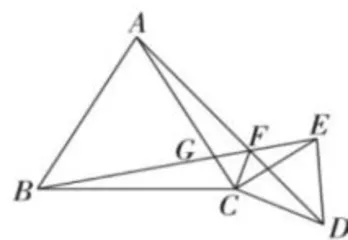
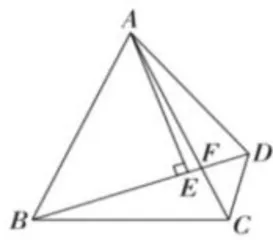
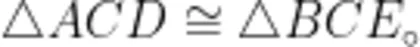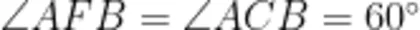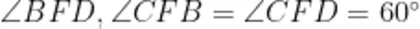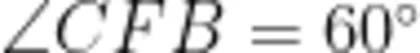模型识别阶段，笔者引导学生找出图1中两个等边三角形的共顶点 C ， 发现 C A 和 C B 长度相等， C E 和 C D 长度相等，其夹角也相等的典型特征。方法提炼阶段，笔者引导学生从共顶点入手，将共顶点的两组等边以“大手拉小手"的方式重新组合，获得“手拉手”全等即 由此，问题（1）得以解决。证得全等后，笔者引导学生关注“第三边"（“大手小手”之外的边） A D ， B E 的位置关系，根据“8字形”导角可得 ，根据第三边上的高相等可得点 C 到 A D ， B E 的距离相等，进而通过证明得出 F C 平分 ，最后基于 ，在 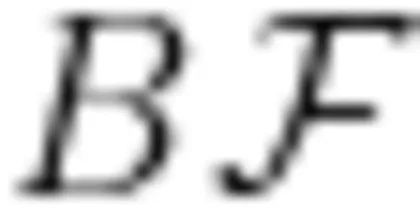上截取线段 F P . 使 F P = F C ，构造等边 Δ P C F ， 完成问题（2）的证明。对于问题（3），基于前两问中的"旋转手拉手”全等和条件 A B = A C 笔者引导学生在 B D 上取点 K ， 使 A K = A D ，构造“旋转手拉手”全等即 Δ A B K ≅ Δ A C D ，并进一步求解。结论梳理阶段，笔者引导学生归纳解题思路：“SAS”证全等 全等三角形的第三边 A D 和 B E 相等 第三边夹角 ∠ A F B 等于旋转角 ∠ A C B 第三边的交点与共顶点的连线 F C 平分第三边的夹角 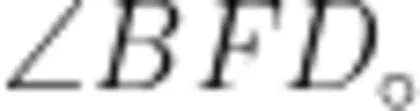体系建构阶段，笔者引导学生从以下三个方向拓展学习。

方向一：婆罗摩笈多模型。如图4所示，点 C 是两个等腰直角三角形共有的直角顶点，“大手” C A ， C B 和“小手” C D ， C E 由原来的标准"手拉手"变为错位“手拉手”，可得如图5所示的两个新的三角形，即 Δ B C D 和 Δ A C E ，这就是婆罗摩笈多模型。其常常涉及如下结论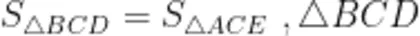： 中第三边 B D 上的中线长度等于 Δ A C E 中第三边 A E 长度的一半，且 B D 上的中线垂直于 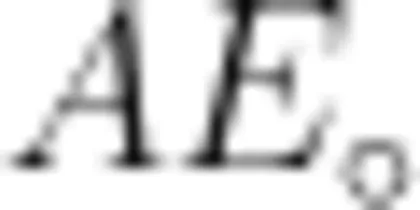此外，教师还可以将条件“ 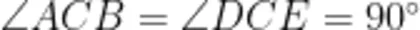”变为一般条件“ ∠ A C B + 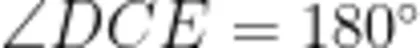”，让原模型变成如图6所示的旋补四边形（两三角形顶角互补的普通等腰三角形共顶点），进而引导学生建立通用模型。

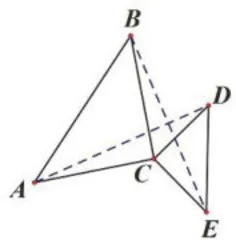
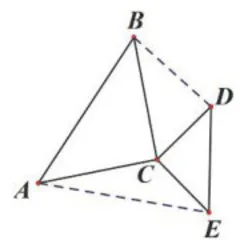
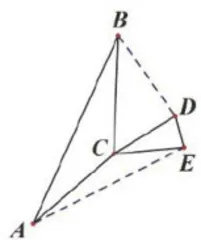
方向二：全等变相似。例如，把图7所示模型的条件 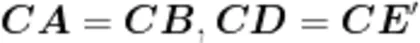变为“ 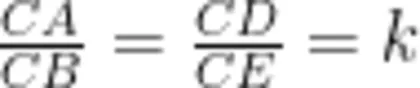”的普通关系（如图8），则 Δ B C E ≅ Δ A C D 变成 Δ B C E ～ Δ A C D 从而将“手拉手"全等归纳为“手拉手"相似的特殊情况，实现从特殊到一般的过渡。