小学数学除法运算大单元教学举措

除法作为乘法的逆运算，其核心在于计数单位的合理分配与转化。除法运算教学要以计数单位为线索，帮助学生构建除法运算知识网络。教师应立足结构化视角创设真实问题情境，借助直观模型引导学生在操作中理解除法的意义和算理，在应用中体会除法与减法、乘法等的内在关联，感悟运算本质上的一致性，增强运算能力和推理意识。本期，我们讨论大单元背景下除法运算教学的整体设计与实施。

大单元教学是提升教学质量、培养学生核心素养的重要途径。本文聚焦小学数学除法运算，探讨大单元背景下如何以计数单位为线索，通过结构化设计与教学，帮助学生构建系统的除法知识体系，深入理解除法运算本质，提高运算能力和推理意识。

一、以计数单位为核心构建除法知识网络

1.整数除法：计数单位的初步理解与运用

整数除法是学生接触除法运算的起点，其算理基于计数单位的平均分。以 3 6 ÷ 3 为例，36由3个十和6个一组成，计算时要先将3个十平均分成3份，每份得1个十，即 3 0 ÷ 3 = 1 0 ；再将6个一平均分成3份，每份得2个一，即 6 ÷ 3 = 2 ；最后将所得结果相加，得出最终结果12。教学过程中，教师可让学生实际操作——将36根小棒平均分成3堆，直观感受分配过程，理解整数除法是对计数单位“十"和“一"的合理分配，初步建立除法运算与计数单位之间的联系。

2.小数除法：计数单位的拓展与深化

小数除法是整数除法的延伸，其教学关键在于将小数转化为相同计数单位的整数后计算。例如，计算 2 . 4 ÷ 0 . 3 时，把2.4和0.3分别转化为以0.1为计数单位的数，即24个0.1和3个0.1，此时小数除法就转化为 2 4 ÷ 3 的整数除法。教师可利用数轴、方格图等直观模型辅助教学。如，在数轴上以0.1为刻度，从0开始标记，让学生观察代表2.4的长度包含几个代表0.3的长度；在方格图中将一个大正方形看作1，把它平均分成10格，每格是0.1，2.4可以用2个大正方形和4个小格表示，0.3可以用3个小格表示，最后通过涂格的方式演示 2 . 4 ÷ 0 . 3 的计算过程。这样教学，学生就能理解小数除法中计数单位换算与运算的本质，体会小数除法与整数除法在计数单位运用上的一脉相承。

3.分数除法：计数单位的灵活运用与升华

分数除法的算理相对抽象，其教学核心在于对分数单位的理解和运用。以 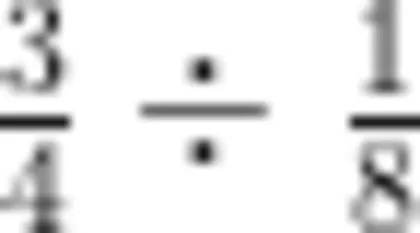为例， 的分数单位是 ，表示有3个这样的分数单位； 是除数的分数单位。计算时，我们可以将 转化为以 为分数单位的数，即 ，此时除法就变成求 里包含几个 ，结果为 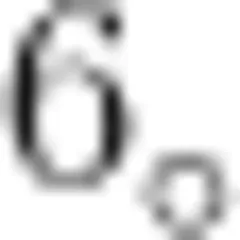教学中，教师可引导学生通过折纸、画图等方式理解算理，如将一张纸平均分成4份，取其中3份表示 ，再将这张纸平均分成8份，看 包含几个 ，进一步体会分数除法与整数、小数除法在计数单位层面的内在联系。

二、结构化视角下的除法教学策略

1.创设真实情境，激发探究欲望

在教学整数除法的过程中，教师可创设“班级组织活动，要将36个气球平均分给3个小组，每个小组能分到几个气球？”的问题情境，让学生在解决实际问题的过程中理解整数除法的“等分除"意义。在教学小数除法时，教师可以设计“苹果每千克2.4元，妈妈买苹果花了12元，她买了多少千克苹果？”的问题情境，引导学生将生活问题转化为数学问题，思考如何运用小数除法解决问题，理解小数除法中“包含除”的意义。在教学分数除法时，教师可以创设“用 千克面粉制作小蛋糕，每个小蛋糕需要 千克面粉，这些面粉能做几个小蛋糕？”的问题情境，让学生在熟悉的生活场景中感受分数除法的应用价值，探究分数除法的计算方法。

2.借助直观模型，深入理解算理

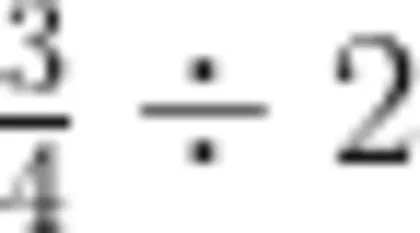直观模型是帮助学生理解数学概念和算理算法的有效手段。在整数除法教学中，教师可运用小棒教学，让学生清晰地看到分的过程和每一份的数量，从而理解整数除法的运算过程。在小数除法教学中，教师可利用米尺模型引导学生理解长度单位的换算与小数除法的关系。如，“1.5米的绳子，平均分成3段，每段长多少米？"教师可演示在米尺上找到1.5米的位置，再将其平均分成3份，直观得出每段长0.5米的过程，帮助学生理解小数除法的算理。在分数除法教学中，教师可使用圆形或长方形纸片作为直观模型。例如，将一张圆形纸片平均分成4份，取其中3份叠在一起表示 ，再将其平均分成2份（相当于计算 ），取其中1份作为结果，学生就能直观地看到每份是 ，从而理解分数除法的算理。

3.引导类比学习，促进知识迁移

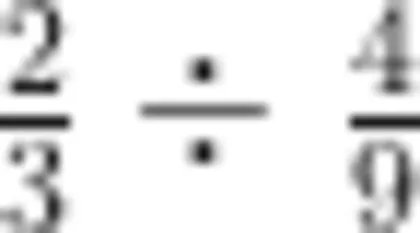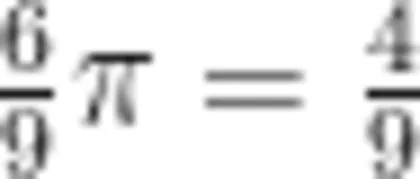在除法运算教学中，教师应引导学生从整数除法运算经验出发，类比探究小数、分数除法算理，感悟运算本质上的一致性。在学习小数除法前，教师要先引导学生复习整数除法的计算方法和算理，如计算4 8 ÷ 4 要从高位除起、数位要对齐等。然后，教师提问：“如果算式是 4 . 8 ÷ 4 ，计算方法与 4 8 ÷ 4 相比会有什么相同点和不同点呢？”教师以此引导学生思考如何将整数除法的计算方法迁移到小数除法运算中，理解小数除法同样要从高位除起，只是要注意小数点的位置对齐。在学习分数除法时，教师要对比整数、小数除法中对计数单位的处理方式，启发学生思考分数除法中如何利用分数单位进行运算。例如，教学 时，教师可引导学生先将 和 转化为相同分数单位的分数，即 ，再进行计算，让学生体会到不同类型除法在算理和算法上的一致性。

4.对比归纳，突出知识本质特征与内在联系

对比归纳是深化知识理解的重要环节。在教学过程中，教师应组织学生对比“包含除”与“等分除”在整数、小数、分数除法中的表现形式和内涵差异。例如，整数除法 2 4 ÷ 6 可理解为求24里包含几个6（包含除），也可以理解为把24平均分成6份，求每份是多少（等分除）；小数除法 3 . 6 ÷ 0 . 6 同样有这两种理解方式。通过对比，学生能明白虽然它们的意义表述形式不同，但本质都是细分计数单位的运算。同时，教师可引导学生归纳商不变规律在不同数域除法中的体现。如，在整数除法中， 1 2 ÷ 3 = （ 1 2 × 2 ） ÷ （ 3 × 2）；在小数除法中， 1 . 2 ÷ 0 . 3 = （ 1 . 2 × 1 0 ） ÷ （ 0 . 3 × 1 0 ） ；在分数除法中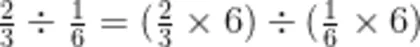， 。这些实例有助于学生总结、归纳商不变规律，体会这一规律在除法运算中的普遍性和重要性，进一步理解除法运算本质上的一致性。

5.拓展应用，体会除法与其他运算的内在关联

此环节，教师可设计综合性问题，让学生在解决问题的过程中体会除法与减法、乘法等的内在关联，感悟运算本质上的一致性。例如，有40个苹果，每次拿走5个，几次能拿完？学生可用除法 4 0 ÷ 5 = 8 计算，也可用减法 4 0 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 = 0 解决，进而体会到除法是相同减数连减的简便运算。

（作者单位：十堰市房县实验小学）