立足单元整体深入理解除法意义

人教版数学二年级下册“表内除法"单元《除法的初步认识》设置有5道例题，主要包括“平均分"的含义（例1）、“等分"情境（例2）、“包含"情境（例3）、“等分除"（例4）、“包含除"（例5）等内容，问题情境比较零散、繁杂。为实现课程内容结构化，帮助学生深入理解除法的意义，笔者结合学情构建理解运算一致性的逻辑框架，并基于单元整体教学提出课程内容重构策略。

一、构建理解运算一致性的逻辑框架

笔者立足大单元整体教学，挖掘出如下助力学生理解运算一致性的教学关键点。

抓住内容结构的一致性。本节内容中，平均分的概念、类型与除法的两种模型具有内在一致性。平均分的两种类型（“包含"和"等分"）聚焦于动作表征，而除法的两种模型（包含除和等分除）聚焦于符号表征和语言表征，教师可通过结构化的情境以及多元表征方式实现知识衔接。

抓住符号表征的一致性。除法是相同减数连减的简便运算，学生在一年级学习的相同减数连减与包含除的问题情境一致。因此，教师可将“相同减数连减”与“除法的初步认识"相结合，沟通除法与减法的关系，实现算式表征的一致性。

抓住数量关系的一致性。两种除法模型涉及的数量关系，如“总数 ÷ 每份数 ⋅ = 份数”及其变式，是所有用除法解决问题涉及的数量关系（如“总价 ÷ 单价 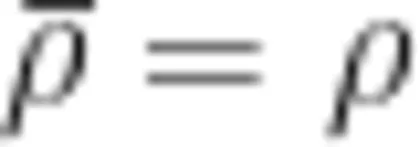数量”“路程 ÷ 速度 时间”及其变式等）的基础。教学除法时，教师说明除法算式中各部分的含义，并提炼、总结除法算式所体现的数量关系，可为学生后续学习用除法解决问题奠定基础。

二、基于单元整体教学的课程内容重构

1.创设情境，序列推进

笔者将教材中4个不同的问题情境（分糖果、橙子、饼干和竹笋）整合为序列化、结构化、生活化的同一个问题情境。例如，创设“分橙子”情境。首先，笔者设置问题“12个橙子，分成3份，可以怎么分？”，引导学生在摆一摆、分一分、算一算中，发现“每份同样多”这一特殊情况，进而揭示“平均分”的概念。其次，承接上述问题情境，笔者将平均分与除法融合，设置如下3个问题情境，序列化推进教学。

问题情境1：将12个橙子平均分，放在3个盘子里，每个盘子里放几个？学生先通过动手操作活动，深人体验平均分的过程，然后通过算一算（列减法算式 1 2 - 4 - 4 - 4 = 0 或除法算式 1 2 ÷ 3 = 4 ，沟通减法和除法的关系，并认识除法算式各部分的名称12是被除数、3是除数、4是商。最后，笔者引导学生基于除法算式中各部分的含义，提炼出“等分除”的数量关系“总数 ÷ 份数 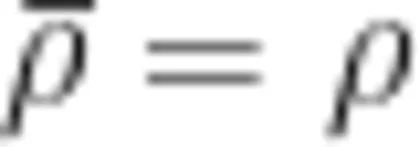每份数”。问题情境2：将12个橙子平均分，放在4个盘子里，每个盘子里放几个？此情境是对上例“等分除"的巩固练习。学生在自主探索中发现，把12个橙子平均分成4份，每份是3个，列算式为 1 2 ÷ 4 = 3 （个）。问题情境3：有12个橙子，每3个放一盘，可以放几盘？学生自主迁移前面解决问题的经验，通过实物、图示、语言等表征方式，抽象出除法算式“ 1 2 ÷ 3 = 4 （盘）”，理解该问题的实质就是求“12里面包含几个3”，并基于除法算式的含义提炼出“包含除”的数量关系“总数 ÷ 每份数 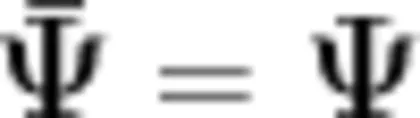份数”。结构化、序列化的问题情境能消除碎片化例题编排的不利因素，促进学生建立知识结构，形成结构化思维。

2.多元表征，促进理解

为帮助学生深入理解"平均分"以及“除法"等抽象概念，笔者通过多元表征方式，让学生经历从具体到抽象的认知过程。以教学“等分除"（问题情境1）为例，笔者采取摆一摆、画一画、理一理、算一算、说一说的步骤教学。

首先，笔者让学生动手操作，摆一摆、分一分，边摆边说分法。学生发现每个盘里应放4个。然后，笔者让学生拿出学习单，在点子图上圈一圈、连一连。完成后，学生交流、评议不同画法（如图1所示4种画法），进而发现一个一个地分最不容易出错。

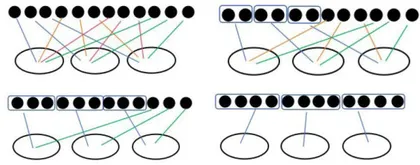
随后，笔者让学生用“是什么？怎么分？结果怎样？”梳理平均分的过程和结果。通过对比不同分法，学生发现虽然分的过程不一样，但分的结果相同——都是将12个橙子平均分成3份，每份是4个。学生在学习单上尝试用算式表示平均分的过程和结果，交流所列出的算式 1 2 - 4 - 4 - 4 = 0 和 1 2 ÷ 3 = 4。在此基础上，笔者引导学生认识“ ÷ ”，掌握除法算式的读法和每个部分的名称。最后，笔者引导学生对照点子图，分别说出算式中的每个数所表示的含义。学生通过观察、思考，得出“12表示一共有12个橙子，即橙子的总数；3表示平均分的份数；4表示每份有几个，即每份数”，并由此抽象出数量关系“总数 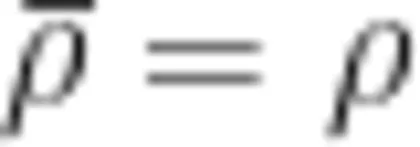÷ 份数 每份数”。

情境2、情境3的教学可仿照以上教学过程进行。教学过程中，笔者注重通过对比，沟通不同情境之间的联系和不同表征方式之间的联系，帮助学生感悟除法的本质。例如，笔者引导学生对比情境1和情境3，发现其相同之处在于“都是平均分，除法算式相同”；其不同点在于“ ① 平均分的方式不同，情境1是均匀地分成若干份，即‘等分’，而情境3是求‘12里包含几个3’，即‘包含分’； ② 算式表示的含义不同，平均分的结果不同，减法算式和数量关系也不同，即情境1是已知总数和份数，求每份数，而情境3是已知总数和每份数，求份数”。对比情境2和情境3，学生发现它们的相同点在于“减法算式相同，都是平均分，都用除法计算，并且分的结果相同”；不同之处在于“平均分的方式不同，算式表示的含义不同，数量关系也就不同”。

3.回归生活，发展思维

为发散学生思维，达到学以致用的目的，笔者布置如下2道练习题。

第1题：仿照上述情境，从 1 2 ÷ 3 = 4 和 1 2 ÷ 4 = 3 中任选一道，创编几个不同的除法故事。以 1 2 ÷ 3 = 4 为例，学生联系真实生活情境，结合除法的含义，编出了多样的数学故事： ①1 2 个小朋友玩游戏，每3人为一组，可以分成4组； ② 将12颗糖平均分给3个小朋友，每个小朋友分得4颗； ③ 明明要读12页书，每天读3页，需要读4天； ④ 将12朵花插到3个花瓶里，每个花瓶里的花一样多，可以插4个花瓶。笔者引导学生对所编的故事进行分类。学生将 ①③ 归为“包含除”， ②④ 归为“等分除”。笔者追问：为什么故事内容不同，却都能用同一道除法算式表示呢？受此启发，学生感悟到除法算式的简洁性与除法意义的丰富性。

第2题：根据图2自主提出与加减乘除有关的数学问题，并列式解决。

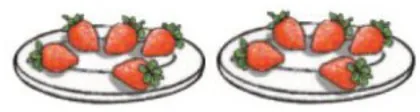
有的学生从“合”的角度提出“一共有多少颗草莓？”，并列出算式 5 + 5 = 1 0 或 5 × 2 = 1 0 。有的学生从“分”的角度提出诸多数学问题并解答： ① 一共有10颗草莓，第一盘有5颗，第二盘有几颗？（10-5=5）。② 一共有10颗草莓，每5颗装一盘，可以装几盘？0 1 0 ÷ 5 = 2 。 ③ 一共有10颗草莓，平均放到2个盘里，每个盘里放几颗？（ 1 0 ÷ 2 = 5 。最后，笔者引导学生寻找上述算式之间的联系。学生通过小组交流，发现除法是减法的简化运算，是乘法的逆运算。

（作者单位：武汉市光谷豹子溪小学）