以有余数除法为锚点创新设计单元教学

本文针对有余数除法教学的现实困境，设计以“分物决策"为核心的大单元教学，基于“班级研学物资优化分配"大任务，从具身化操作、决策思维培养、跨学科联结三个方面设计教学活动，使学生在解决序列化问题的过程中提升估算、试商、验算等运算能力，并创新设计素养导向的评价方式。

一、有余数除法教学的现实困境

1.认知断层现象

学生学习有余数除法时往往会出现认知断层问题。武汉市某小学二年级10个班的问卷调查结果显示， 6 5 % 的学生能准确计算 2 3 ÷ 5 = 4 ⋅ s 3 ”，但对“23块饼干，每人分5块，最多能分给几人？"这类实际问题， 3 8 % 的学生错误地选择"5人”。这一现象揭示出学生存在算法与算理脱节的问题。深入追踪发现，学生脱离具体分物情境列竖式计算时，计算错误的学生中有一半以上的学生难以解释余数必须比除数小的内在逻辑。这说明算法操作与意义建构之间的失衡，导致"实物一表象一符号"的认知链难以形成。

2.问题情境割裂

现行教材在有余数除法内容的编排上存在问题情境离散情况。如人教版教材横跨3个单元分散呈现7类有余数除法应用题，如“分铅笔”“租船问题”“周期问题”等。这种编排方式导致例题相互孤立，缺乏一个贯穿始终的任务情境。这可能导致学生机械记忆不同情境问题的解题套路，难以建立一套通用的"余数处理策略”。调研发现，学习“周期问题”后，仅 3 7 % 的学生能自主迁移分物经验，通过计算解决“第38朵花是什么颜色"这类问题；大多数学生仍然依赖绘制完整周期图的策略解题。这些现象反映出离散情境教学导致的学生思维迁移受阻困境和解题策略固化危机。

3.评价导向偏差

对有余数除法的考查往往过度依赖计算正确率、解题速度等量化指标，而要求学生阐明余数实际价值的开放性试题占比不足且多为附加题。这种评价导向可能导致余数处理逻辑解释能力、方案优化意识等处于监测盲区，不被教师和学生重视。有余数除法相关题目缺乏对"是否需要进一""怎样调整方案”等决策层级设问的评价偏差，催生了“虚假问题解决"的教学怪圈。对“用载重6吨的卡车运输32吨货物"的典型案例， 7 3 . 9 % 的五年级学生仅满足于呈现 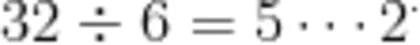的计算过程，而不去考虑“剩余货物需再派1辆车运输”的实际工程方案。这体现了评价维度残缺对学生数学建模能力发展的制约。

二、以“分物决策”为核心重构概念网络

1.锚定单元核心概念

教师以“有限资源的公平分配与数学表征"为核心，构建如下大单元教学概念体系。

分物公平性 整除与余数的产生 余数的数学表达↓

与分数除法的联结 余数处理策略 现实决策需求（进一法/去尾法/分数表示）

从学科本质看，这一概念体系聚焦数学建模过程，将分物活动解构为“现实问题数学化一数学问题现实化"的过程。“余数处理策略"作为联结抽象计算与真实情境的枢纽，要求学生突破机械运算的局限，在解决实际问题的过程中发展决策能力。例如，对“48人乘船游湖，每船限载6人，需要几条船"而言，余数“0"在数学计算上看似完美，而在实际决策中却要考虑安排空船以保障安全等现实因素。这要求学生深刻理解数学解题严谨性与现实决策灵活性之间的辩证关系。此外，该概念体系延伸至分数除法，设置了“有余数除法结果的分数表示"认知接口。

2.设计贯通性单元任务

为帮助学生理解和应用有余数除法知识，教师针对四年级学生设计了贯穿大单元教学的“班级研学物资优化分配"大任务。该任务分8个课时实施，其实施阶段、数学焦点和相应的素养目标如表1所示。

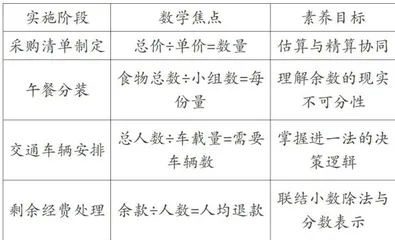
采购清单制定阶段要解决单价与数量的精算问题。教师依托“用200元班费采购单价6元的笔记本，可以买多少本？"问题情境，引导学生先计算得出4 2 0 0 ÷ 6 = 3 3 （本）…2（元）”，然后讨论余数“2元"如何处理、最终结果是33还是34。有的学生用估算方法验证，因为 6 × 3 3 ≈ 1 8 0 ， 1 8 0 < 2 0 0 ，所以确认33本的价格在预算范围内；有的学生提出增补4元（ 6 - 2 = 4 预算，加购1本以更好地满足分配需求的想法；还有的学生提出可以把剩余的2元留作备用金，以应对后续物资增补需求。午餐分装阶段的目标是理解余数的现实不可分性。教师基于情境“17份盒饭平均分给5个小组，每组分得3份，还余2份"提问：剩余2份能否拆分？学生通过分餐过程演示，明确余数需保留，深化了对体现余数的现实不可分性问题的理解。交通车辆安排阶段的目标是明确进一法的决策逻辑。教师呈现问题情境：43人乘车，每辆车最多能坐9人，需要安排多少辆车？学生计算得出‘ 4 3 ÷ 9 = 4 （辆）7（人）”后，教师引导学生讨论4辆车够不够。学生发现余下的7人仍需1辆车来载，所以结果是5辆，从而深入理解了进一法源于现实需求。剩余经费处理阶段要关注小数与分数的联结。教师创设“结余的13元要平均分给8人"的问题情境。学生计算得出每人分得“1.625元”（ 1 3 ÷ 8 = 1 . 6 2 5 后，教师引导他们用分数表示结果。学生写出 出1后，教师引导其对比两种表征方式的差异。学生发现1.625元可看作1元6角2分5厘，直观表示具体数值;而13能清楚地表示把13元平均分成8份。后续，学生在教师点拨下理解了小数与分数的等值关系，为继续学习两者的转化打下了基础。

四个阶段以余数为线索展开，形成“计算（采购） ↦ 理解（分装） 应用（车辆） ↦ 拓展（经费）"的教学逻辑，体现了从知识习得向能力迁移的跨越。

三、教学实施的三重突破

1.具身化操作：从具象到符号的认知脚手架

动态分物实验。为帮助学生更好地理解有余数除法的概念，教师紧扣午餐分装阶段核心内容“食物总数 ÷ 小组数 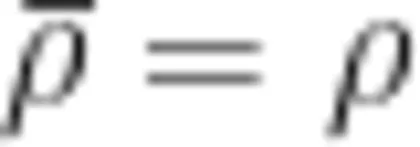每份量”，设计“23块饼干平均分5组”的实验，并用磁性圆片和分隔板作为教具。实验分两个阶段。第一阶段通过直观操作感知余数存在。学生用磁性圆片代表饼干，用分隔板划分出5个组别，通过逐一分发操作，得出每组分得4块，还剩3块，以此呈现分物后余数的实际状态，并同步记录算式 5 × 4 = 2 0 。第二阶段制造认知冲突揭示余数边界。在尝试给每组追加1块饼干时，学生发现需要5块饼干，但手中仅剩3块。这个矛盾点或者说决策点出现后，教师引导学生通过对比观察生成“余数 < 除数"的关键认知，明确了余数的取值范围。

数形结合建模。针对学生在运算中暴露的竖式对位错乱、单位混淆等问题，教师引导学生通过数形结合构建模型来解决。教师以"23块饼干平均分给5人"的情境为载体，通过标记法帮助学生实现具象操作与符号表征的协同。例如，教师用绿色色块标记分物过程，每完成一组分配，便在竖式计算结果中商的个位数字处涂色，帮助学生建立“商的个位数值与实际分配份数的个位数值对应”的认知；在分物操作与算式书写时同步标注“块”，通过“分掉20块"的阶段性标记强化单位识别。

2.决策思维培养：从算术到策略的升华设计变式问题链。在交通车辆安排阶段，为了培养学生的决策思维，提高其在不同情境下灵活运用余数处理方法的能力，教师设计了阶梯式问题组。

基础题：27名学生乘车，每辆车限乘6人，需要几辆车？这个问题引导学生用进一法计算 [ 2 7 ÷ 6 = 4 （辆）3（人），得出需要5辆车的结论，强调实际生活中涉及人身安全的问题不可突破底线。

对比题：用27元购买单价6元的笔记本，最多买几本？此问题要求学生用去尾法计算 [ 2 7 ÷ 6 = 4 （本）3（元），得出4本的结论，有助于其理解资源受限情况下，不能超出实际可支配资源来分配。

拓展题：用27分钟做6分钟/次的健身动作，能做几组？这个问题旨在引入连续量测量的概念，学生可用小数或分数表示结果，如 2 7 ÷ 6 = 4 . 5 （组）。

变式问题引导学生在真实情境中理解余数处理方法的多样性，增强其根据不同情境合理决策的能力。

提炼决策依据。在剩余经费处理阶段的总结环节，教师引导学生建立余数处理方法的“三维度"判断准则。维度一是资源性质，即判断资源是可拆分还是不可拆分。例如，车辆座位属于不可拆分资源，而货币可以找零，属于可拆分资源。我们处理余数时要根据资源的性质选择合适的方法。维度二是安全要求，如车辆不得超载，必须优先考虑安全因素，因此要采用进一法解决问题。维度三是结果精确度需求，即判断是否允许用分数表示结果。例如，健身动作组数的计算允许半组的存在，此时可以用分数表示结果。综合考量三个维度，学生就能准确选择合适的余数处理方法，形成余数处理策略，提高决策思维能力。

3.跨学科联结：从数学到生活的意义重构

以计算机科学启蒙跨学科学习活动为例。在交通车辆安排阶段，教师通过Python代码演示余数运算在循环队列座位分配算法中的实际应用。教师先呈现问题：“23名学生按每组5人入座，如何快速确定每个人的组号与座位号呢？”接着，教师让学生尝试手动分组，暴露效率低的问题，自然引出编程解决方案。然后，教师进行代码拆解与可视化演示，最终在编程平台上写出如下代码。

python students=23

group_size=5 for i in range（students）：

group=i//group_size position=i%group_size

print（f"学生{i}→第{group + 1}组第{position + 1位"）

这段代码会从第0名学生开始，一直到第22名学生，逐个为他们确定所在小组和组内位置。对于每名学生，代码要做两件事。一是计算该生所在小组，用该生编号（i）除以每组人数（5），取商的整数部分，得出组号，用这个组号加1得出实际组号。如编号8的学生，8除以5，商是1，可得他在第2组。二是计算该生的组内位置，用该生编号除以每组人数，取余数，用余数加1可得其组内位置。同样以编号8的学生为例，8除以5，余数是3，可得他在组内是第4个位置。最后，教师引导学生修改参数，如students=37、group_size ： = 6 等，观察余数变化对分组的影响等。

四、素养导向的评价创新

教师通过测试、课堂观察、数据分析和访谈等方式评价学生学习效果。在单元后测中，教师发现学生的策略迁移能力与前测相比显著提高， 8 5 % 的学生能自主将“车辆调度"的经验迁移到“疫情物资发放”等新情境中，并且最优方案产出率达到 6 3 % ，这说明学生能灵活运用所学知识解决实际问题。课堂观察结果显示，学生在实物操作环节能准确解释商与余数的关系。通过课后访谈，教师发现 8 2 % 的学生能举例说明“余数必须比除数小"的实际意义，这表明学生透彻理解了算理。

教师还引入“余数决策能力雷达图"形成性评价系统，构建学习过程的动态监测机制。系统通过采集学生的解题策略选择轨迹、错误修正日志及方案陈述视频等多模态数据，从计算准确性、策略合理性、方案创新性、表达严谨性四个维度生成可视化评估结果。学生可通过雷达图了解自身优势与短板，开展靶向训练。

（作者单位：武汉市光谷第二初级中学）文字编辑刘佳