数形结合提升思维品质

六年级是培养学生思维能力的关键阶段，教师应有意识地在教学中渗透数形结合思想，引导学生更好地把握数学问题的本质，提高思维品质。

数形结合理解算理。教学分数乘法时，教师可以先展示本节课相关的图形和算式，让学生思考图形与运算之间的关系，然后呈现“求一个数的几分之几是多少”的问题情境，引入 三个算式，最后引导学生画出对应的图形（如图1）。

从图中，学生可以清晰地看到每个部分所代表的数值，进而直观地理解算理，掌握计算方法。

数形结合发现规律。数形结合是打开数学规律的一把钥匙。通过将数字序列转化为图形坐标，或在几何图形中寻找代数规律，学生能直观感受抽象概念的本质，发展空间观念和模型意识。

教师先展示教材的例题（如图2），引导学生仔细观察方块的数量和排列方式，思考图和算式的关系，并把算式补充完整。

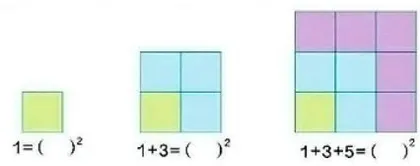
接着，教师提出问题：“图片中第一个方块数量与第二、第三个方块数量之间有什么关系呢？"学生发现第一个方块只有1个小方块，第二个方块由4个小方块组成，第三个方块由9个小方块组成。为了引导学生发现规律，教师提出问题：“通过观察不同颜色的方块数量，大家能发现方块数量与对应算式之间的关系吗？”这个问题激发了学生的探究欲望，他们开始尝试将方块数量与算式联系起来，通过画图、做标记等方式辅助思考。在教师的引导下，学生逐渐发现了规律：第一个方块的数量1即1表示，第二个方块的数量可用 1 + 3 即 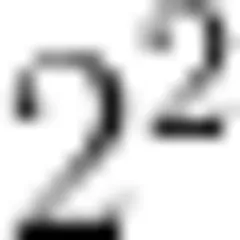表示，第三个方块的数量可用 1 + 3 + 5 即 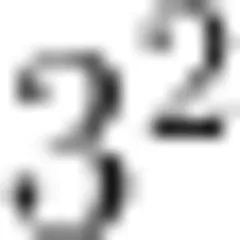表示，也就是说，小方块的数量等于算式中加数个数的平方。

数形结合提升解决问题能力。小学数学教学中，教师应该充分利用数形结合的方法，帮助学生更好地掌握数学知识和技能，提高解决问题的能力。

例如，教师出示以下例题：“上午8点8分，小明骑自行车从家里出发，8分钟后，爸爸骑摩托车在距离家4千米的地方追上了他，然后爸爸立即骑摩托车回家，到家后又立刻回头再追小明，这次追上小明时，恰好距离家8千米，这时是几点几分？"学生读题后，教师通过“以形助数"的方法，请学生画出小明和爸爸行驶的路程图，清晰地看到两人行驶的时间、速度和路程关系（如图3）。

学生发现，从爸爸第一次追上小明到第二次追上小明，小明骑行了 8 - 4 = 4 千米，爸爸骑行了 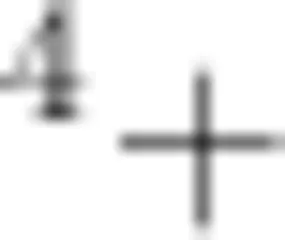8 = 1 2 千米，由此可知爸爸骑摩托车的速度是小明骑自行车速度的3倍（ 1 2 ÷ 4 = 3 ）。接着，学生按照这个速度关系计算，如果小明骑行8千米，那么爸爸可以骑行 8 × 3 = 2 4 千米，但从现实情况看，爸爸没有用到那么多分钟。由题干可知，爸爸少用了8分钟，因此爸爸骑行了 4 + 1 2 = 1 6 千米，而少骑行了 2 4 - 1 6 = 8 千米。由此，学生用 8 ÷ 8 = 1 计算出摩托车的速度是1千米/分，那么爸爸骑行16千米就需要16分钟，所以总计时间为 8 + 8 + 1 6 = 3 2 分钟，即时间为8时32分。

（作者单位：枣阳市第四实验小学）