小学数学分段计算问题教学策略探究

分段计算问题是增强学生应用意识的重要抓手，也是激发学生创新思维、提升学生数学语言表达能力的有效途径。

紧密联系生活实际。分段计算问题教学应与生活实际紧密结合，让学生感受数学的实用性，提升解决问题的能力。以水费计算题为例：“某市规定每月用水量不超过20吨按每吨3元收费，超过部分按每吨4元收费。明明家8月份用水32吨，应缴纳水费多少元？"教师可引导学生分三步计算：先计算基础用量20吨的费用（ 2 0 × 3 = 6 0 元），再计算超出部分12吨的费用（ 1 2 × 4 = 4 8 元），最后将两部分相加得到该月水费（ 6 0 + 4 8 = 1 0 8 元）。

在此基础上，教师出示燃气费计算题：“某市燃气每月收费标准为0＼～100立方米的部分每立方米2元，101＼～200立方米的部分每立方米2.5元，超过200立方米的部分每立方米3元。某家庭月用气量230立方米，应缴纳燃气费多少元？"学生小组交流后，汇报“分段累加"的计算思路：第一段100立方米费用为 1 0 0 × 2 = 2 0 0 元，第二段100立方米费用为 1 0 0 × 2 . 5 = 250元，第三段30立方米费用为 3 0 × 3 = 9 0 元，最后用2 0 0 + 2 5 0 + 9 0 = 5 4 0 元得出总费用。

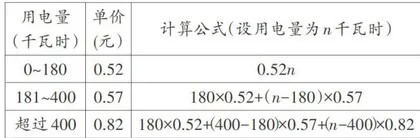
创设解法多样的问题情境。教师可以创设具有挑战性的分段计算问题情境，鼓励学生从不同角度探索解决方案，培养创新思维。以电费计算题为例：“某市采用阶梯电价：月用电量180千瓦时以内按0.52元/千瓦时计算，181＼～400千瓦时的部分按0.57元/千瓦时计算，超过400千瓦时的部分按0.82元/千瓦时计算。某户居民某月电费162元，求当月用电量。"学生通过合作学习与讨论，得出如下3种解决方法。一是方程法。设用户当月用电量为 x 千瓦时，建立方程求解。学生假设 x 在第二档（ 1 8 0 < x⩽4 0 0 ），列方程 1 8 0 × 0 . 5 2 + （ x - 1 8 0 ） × 0 . 5 7 = 1 6 2 ，解得 x = 3 0 0 ，验证其符合第二档范围。二是推理法。学生先假设用户用电量未超过180千瓦时，那么最多花费 1 8 0 × 0 . 5 2=9 3 . 6 元，

9 3 . 6 < 1 6 2 ，说明用电量超过180千瓦时；接着计算180＼～400千瓦时部分的费用， 4 0 0 - 1 8 0 = 2 2 0 千瓦时，因此这部分最多花费 2 2 0 × 0 . 5 7=1 2 5 . 4 元， 9 3 . 6 + 1 2 5 . 4 = 2 1 9 元，219元 > 1 6 2 元，说明用电量没超过400千瓦时；因为超出180千瓦时的部分花费为162-9 3 . 6=6 8 . 4 元，超出部分的电量为 6 8 . 4 ÷ 0 . 5 7 = 1 2 0 千瓦时，所以当月总用电量为 1 8 0 + 1 2 0 = 3 0 0 千瓦时。三是列表法。学生列出如下表格，并通过计算和推理解决了问题。

通过对比交流不同方法，学生不但掌握了解决复杂问题的方法，而且培养了创新能力。

强化数学语言表达训练。在分析分段计算问题时，学生需要运用数学语言准确描述数量关系、计算过程和解题思路。以水费计算为例，学生应完整表述：“根据阶梯水价标准，先将总用水量32吨分为20吨的基础用量和12吨的超额用量，分别计算 2 0 × 3 = 60元和 1 2 × 4 = 4 8 元，最后将两部分相加得到总水费108元。"在呈现解题结果时，教师要强调表述的准确性。例如，解决出租车费用问题：“某市出租车收费标准为：3公里内10元；超过3公里至10公里部分，每公里2元；超过10公里部分，每公里3元。若乘客乘坐15公里，应支付多少元车费？"学生需要完整表述计算过程：“前3公里10元；10公里减去3公里得到7公里，第二部分费用为 7 × 2 = 1 4 元；超过10公里的部分有5公里，费用为 5 × 3 = 1 5 元。总费用为 1 0 + 1 4 + 1 5 = 3 9 元。”规范表述有利于提高学生思维的严谨性和逻辑性。

（作者单位：咸宁市实验小学）文字编辑张敏