初中数学个性化导学问题的设计探究

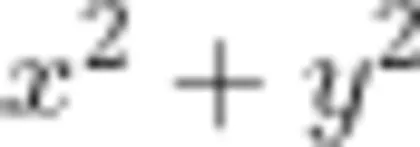
叶澜指出：“差异的存在是公平提出的前提。教育公平的理想式表达是：保障每个人享受教育的平等权利（包括机会、过程和结果）。从差异的角度看，那就是要在承认和尊重差异的基础上，改变不合理的差异，以实现平等。”[1]《义务教育数学课程标准（2022年版）》（以下简称"《义教数学课标》”提出让“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”。因此，在初中数学教学中，教师需要在承认学生数学能力存在个体差异的基础上，促使每个学生都能得到最优发展。个性化导学问题是一种很好的尝试，它是指根据学生已有的思维水平与知识水平的差异，在学生自主学习的过程中提供分层次的问题。其目的是引导学生以问题为主线，以问题解决为驱动，主动参与学习的过程，探究新知识，从而使不同层次的学生都能通过导学问题获得相应的帮助，最终获得成功的体验。

一、个性化导学问题的设计原则

个性化导学问题的主要特点是针对学生差异，以“问”为线索，以“导”为方向，以“学”为目标。这就需要教师在设计问题时，注重以下设计原则。

（一）明确差异，突出阶梯性

在初中数学教学中，明确学生之间的差异并据此设计具有阶梯性的问题，是提升教学质量、促进每个学生个性化发展的关键策略。这一理念不仅体现了因材施教的教育原则，也符合维果茨基的最近发展区理论，即通过设计符合学生当前能力水平并稍具挑战性的任务，激发学生的潜能，推动其认知发展。

在初中数学教学中，学生的个体差异表现在多个方面，包括数学基础、思维能力、学习兴趣和学习习惯等。明确这些差异是设计有效问题的前提。在明确学生差异的基础上，问题设计应突出阶梯性，即按照由易到难、由浅入深的顺序，设计一系列具有层次性的问题。也就是说，教师可以通过尊重个体差异、设计层次性问题、结合多种教学方法和优化反馈机制等方式，促进每个学生的个性化发展和全面提升。

（二）关注兴趣，突出新颖性

关注学生的兴趣并设计新颖的问题，是激发学习动机、增强学习体验、促进深度学习的重要途径。这一设计理念不仅体现了以学生为中心的教育理念，也符合建构主义学习理论，即学习是学习者主动建构知识意义的过程，而兴趣和新奇性是驱动这一过程的关键因素。

在初中数学问题设计中，关注学生的兴趣意味着教师需要了解学生的兴趣点，包括他们喜欢的数学话题、数学游戏、数学史故事等，并将这些元素融人问题设计中。突出新颖性意味着教师需要不断探索和创新问题的呈现方式和解决路径，打破传统的问题呈现模式，以新颖、独特的方式呈现数学问题。也就是说，教师可以通过了解学生的兴趣点，创新问题的呈现方式和解决路径等方式，激发学生的学习动机和探索欲望，促进其深度学习和全面发展。

（三）激发思维，突出开放性

在初中数学教学中，激发学生思维并设计开放性问题，是促进学生高阶思维发展，培养学生创新能力和问题解决能力的关键策略。这一设计理念不仅符合布卢姆的教学目标分类理论，强调从记忆、理解等低阶思维向应用、分析、评价、创造等高阶思维的发展，也体现了建构主义学习理论中关于学习是知识建构过程的观点，强调学习者通过主动探索和问题解决来建构知识。

激发思维意味着在数学问题设计中，要创设能够引发学生深度思考，促进学生思维活动的问题情境。这类问题通常要求学生超越简单的记忆和复述，进人更高层次的思维活动，如分析、评价和创造。开放性问题是指那些没有唯一答案或标准解法的问题，它们通常要求学生进行创造性的思考和探索，以形成自己的理解和解决方案。这类问题能够极大地激发学生的好奇心和探索欲，促进其创新能力和问题解决能力的发展。也就是说，教师可以通过创设问题情境、设计开放性问题、营造创新氛围等方式，促进学生高阶思维的发展，以及创新能力和问题解决能力的培养

二、个性化导学问题的设计策略

在初中数学教学中，设计个性化导学问题是激发学生思维、培养核心素养的有力抓手。下面，笔者根据上述设计原则，结合具体案例，谈谈个性化导学问题的设计策略

（一）基于学生的差异性设计阶梯性问题

阶梯性问题设计是指将复杂问题分解为一系列由易到难、逐步深入的小问题，形成问题链，从而帮助学生逐步建立知识之间的联系，从简单到复杂逐步攀升，最终解决核心问题。教师需要明确学生的数学能力差异，并在突出教学内容的基础上，从易到难设计三至四个富有梯度的问题，以适应不同学生的学习进度和能力水平，使不同层次的学生都能根据自己的实际情况选择相应的问题进行探究，从而更好地激发学习热情，并在积极主动的探究中实现个性化学习。

【案例 1】“ 一次函数的应用探究”阶梯性问题设计

[第一阶梯：基础应用]

1.已知函数 y=2x+1 ，你能否完成有序数对的表格填写？2.你能根据表格绘制函数图象，并指出图象经过的象限吗？

[第二阶梯：理解提升]

3.某快递公司首重收费规则为：基础价（ 1kg 以内）5元，每超重 1kg 加收2元且不足1kg 的按 1kg 计。你能否建立费用 y （元）与重量 x（kg） 的函数关系式？4.若小明需寄 3.5kg 包裹，实际收费能否用该函数精确计算？为什么？

[第三阶梯：综合分析]

5.比较问题1中的函数 y=2x+1 与问题3的快递收费函数，请思考：二者图象形状是否相同？实际应用中的取值限制有何差异？

[第四阶梯：拓展探究]

6.你能否设计一个分段函数来描述新收费规则（ 3kg 以内8元，超出部分每千克加1.5元且不足 1kg 的按 1kg 计）？请用函数图象表示并分析其经济意义。

上述案例在整体设计上遵循皮亚杰的认知发展理论和学生问题解决的心理过程，尊重学生的差异性，引导学生从具体数值计算（第1题）到抽象建模（第3题），经历“具体运算→形式运算”的认知过渡，通过“表格 →图象→实际问题”的渐进路径建立多元表征。同时，该设计也体现了维果茨基的最近发展区理论，如第4题设置“3.5kg这个非常规值，给学生在已知函数基础上制造认知冲突，又如第6题的分段函数设计，为学有余力的学生提供挑战空间。

总体而言，上述案例具有三个特征：一是难度渐进性，从计算维度看，是“整数→小数→非数值分析”，从认知维度看，是“记忆→理解→应用→分析→创造”；二是思维衔接性，第3题的收费模型为第6题的分段函数作铺垫，第5题的对比分析为理解函数本质属性理下伏笔；三是差异化支持，基础层确保全体学生可达基准线，拓展层通过开放性问题（如经济意义分析）实现个性发展。

在设计阶梯性问题时，教师还需关注三个要点：一是搭建概念脚手架，如上述案例通过“表格填写（具象）→图象绘制（半抽象） arrow 模型建立（抽象）”进行三阶过渡；二是认知冲突设计，如第4题暴露函数模型的局限性，引发学生对定义域的思考；三是现实关联度，如第6题要求分析经济意义，体现项目化整合思想。

阶梯性问题的设计通过认知台阶的搭建，既保证了知识体系的完整性，又实现了“低门槛、高天花板”的个性化学习空间，符合《义教数学课标》提出的“面向全体，关注差异”的教学原则。

（二）基于学生的兴趣点设计新颖性问题

新颖性问题设计旨在通过引入新颖、有趣或与学生日常生活紧密相关的情境，吸引学生的注意力，激发他们的学习兴趣和好奇心。这类问题通常能够打破传统教学的框架，让学生在解决问题的过程中体验到数学的乐趣和实用性。

【案例2“勾股定理的跨学科探索”新颖性问题设计

[第一类新颖性：现实情境重构]

1.（数据追踪）某短视频平台上，一条科普视频的点赞数 （x） 与收藏数 （y） 存在关系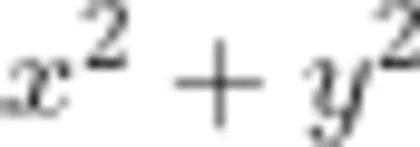： =25z²为分享次数）。若某时刻 z=2 ，点赞数与收藏数均为正整数，你能否求出可能的 （x y 组合？分析当分享次数 z 变化时，点赞数与收藏数的比例关系会如何变化？

[第二类新颖性：跨学科融合]

2.（物理实验）用三根不同长度的吸管制作三角形支架（长度单位： cm ）。若吸管A、B呈直角，长度分别为6和8，吸管C作为斜边时，支架刚好稳定。若将吸管A替换为可伸缩结构（长度 6+k ），吸管B长度保持8不变，你可以分析k的取值范围与支架稳定性的关系吗？

[第三类新颖性：开放答案设计]

3.（考古猜想）古巴比伦泥板记载了几列神秘数字，其中A列是119、3367等，B列是120、3465等，C列是169、4825等。请观察A、B、C列数值规律，能否提出至少两种数学解释？请选择一种解释设计验证方案，并说明其与勾股数的关联。

上述案例在整体设计上遵循建构主义理论并关注数学核心素养导向和学生创新意识培养。如问题1既强调真实数据代入，通过“点赞一收藏一分享”的真实行为数据，将抽象定理具象化为可感知的社会现象，帮助学生建立意义关联，又关注建模思想渗透，通过变量关系分析，将现实问题转化为数学表达式，引导学生理解定理的普适性与边界条件。同时，该设计还体现了多元智能理论。再如问题2的物理稳定性分析，可满足逻辑数学智能（定理应用）身体动觉智能（手工制作）自然探索智能（实验观察）等多维度发展需求。又如问题3的多种解释路径，为语言智能（描述猜想）空间智能（图形验证）等提供差异化呈现方式。

总体而言，上述案例具有三个特征：一是情境创新性，脱离传统“旗杆影子""梯子靠墙”等经典场景，引入数字化生存（社交媒体）工程实践（可伸缩支架）、人文考古等前沿领域，如问题1将勾股数转化为“点赞一收藏一分享”的传播模型，反映网络时代的数学现实意义；二是结构开放性，包括条件开放和结论开放，前者如问题2的吸管长度参数k不预设增减方向，充许正向延长与反向缩短的双向探究，后者如问题3的古巴比伦数字可解释为斜边计算 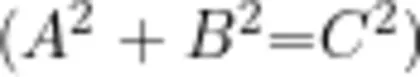或比值关系[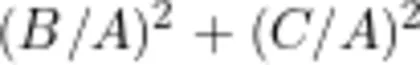 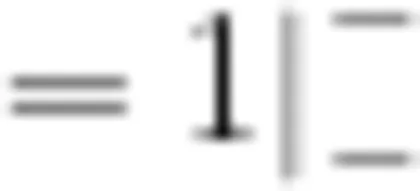等；三是思维非标化，如问题3的验证方案设计涉及反证法、数值模拟、几何作图等多种工具的自由选择。

在设计新颖性问题时，教师还需关注三个要点：一是生活陌生化处理，即将常见现象赋予数学结构，通过非常规参数组合制造认知新鲜感，如问题1中“ 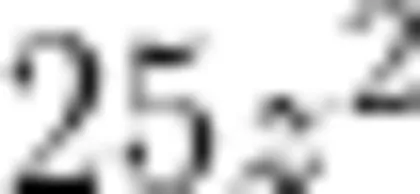”的设计既保持勾股数特性，又暗含“每分享1次带来25倍传播效应”的社会学隐喻；二是学科边界溶解，这又包含物理溶解和历史溶解，前者如问题2，将数学定理与材料力学结合，通过k值变化探讨“刚性三角形 →柔性结构”的临界点，体现STEM整合思想，后者如问题3，通过古代数学文物探究，连接数学史与数论研究，培养跨时空数学思维；三是认知冲突预设，如在问题2中设置“支架稳定性”的工程需求，与纯数学的勾股定理形成张力——数学上成立的三角形（如 6+8>10 ），在物理中可能因 k 值过大导致材料形变而失效。

这种设计通过打破学科壁垒、重构现实情境、设置开放性任务，使传统数学问题焕发新生命力，实现“用旧知识解决新问题，在新场景深化旧认知”的双向促进。

（三）基于学生的创新力培养设计开放性问题

新时代的数学教学，需要引导学生从多个维度思考问题，培养其发散思维能力。开放性问题设计通常要求学生进行创造性的思考和探索，以形成自己的理解和解决方案，能促使学生跳出传统思维模式，培养创新思维和问题解决能力。