回归转化的本源 提升度量的价值

“平行四边形的面积”是多边形面积单元教学的重要一课，是学生正式用转化的方法解决多边形面积的起始课。在教学时，大部分教师都把重点放在如何将平行四边形转化为长方形，进而推导出平行四边形面积的计算公式。这样的教学，过多地突出长度的对应关系，缺少了通过改变度量对象的形状来精确计算不完整面积单位的体验过程，影响了学生对“度量"这一核心概念的感悟和对公式的整体认知。如何基于度量和转化的本质开展平行四边形面积的教学呢？笔者做了如下尝试。

一、回忆旧知，唤醒已有经验

师：同学们，看到图1这份材料，你们明白了什么？

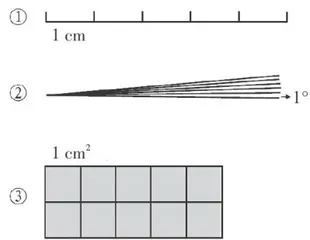
生：每一段长 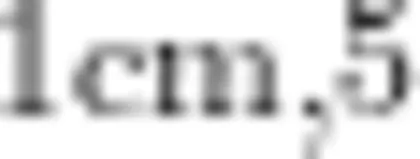段就是 5 c m 。

生：每个小角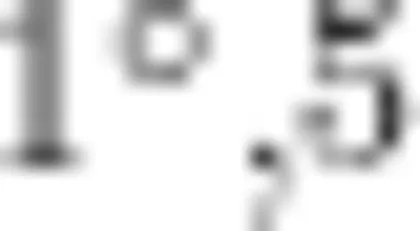是 个小角就是 。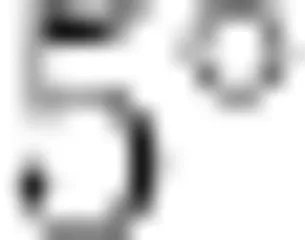

生：每个小正方形面积是 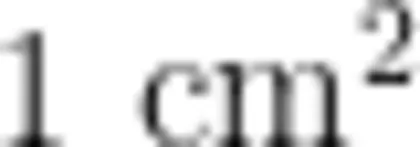，10个小正方形的面积就是 。

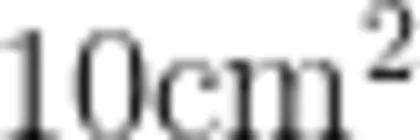师：谁能用一句话来总结刚才三个同学的发现？

生：他们的意思是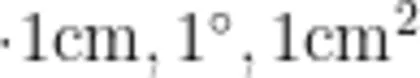， 其实就是一个标准，数出它们的个数，就可以知道线段的长度、角的大小或者长方形的面积。

师：总结得非常好！无论是度量长度、角还是面积，都要先找到一个标准，就是它们的单位，然后用这个单位去度量，数一数共有多少个这样的单位，就能度量出线段有多长、角或者面积有多大。

【思考】学习平行四边形的面积时，学生需要哪些经验？这些经验是怎样获得的？又以怎样的方式唤醒？本教学环节呈现一组结构化的材料，回顾长度、角和面积的度量过程，重点解释长方形面积的推导过程，明确面积的本质就是数有几个单位面积，为本课的教学奠定了基础。

二、自主数方格，理解面积本质

1.顺向引导，再次感受面积的意义

师：同学们，刚才我们已经知道了长方形面积的度量方法。那么，这个平行四边形的面积是多少，你们打算怎样度量？

生：用 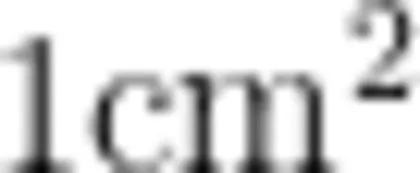的小正方形摆一摆、数一数。

生：把这个平行四边形印到方格纸上，数一数一共有几个小方格。

师（课件呈现，如图2）：你们打算怎么数？（每个小正方边长 ）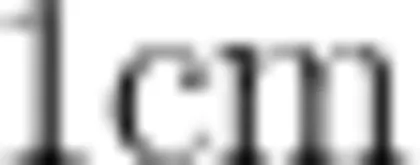

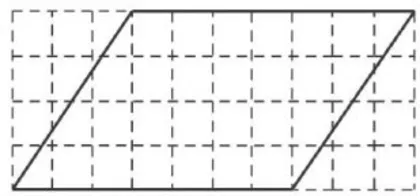
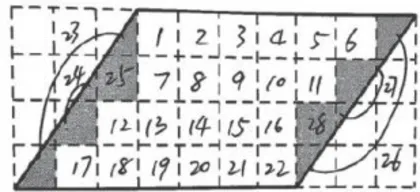
生：如图3所示，我先数完整的小正方形，一共有22个，再数不完整的小正方形，大的和小的拼一下，大概有6个，所以这个平行四边形的面积大概就是 。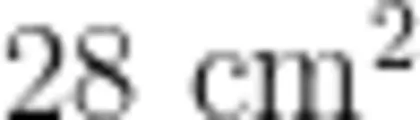

师：也就是说，这个 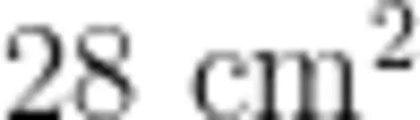是你们

生：估算的。

师：实际面积可能比 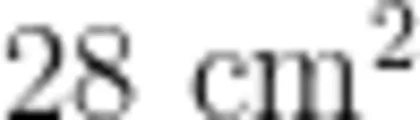大，也可能比 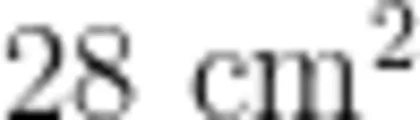小，当然也可能相等。

师：大家回想一下，刚才我们度量长方形面积时，有没有估算？

生：没有。因为长方形的每个方格都是完整的。

师：我明白大家的意思了。当我们用小正方形作为面积单位，去度量一个多边形的面积时，如果所用的小正方形都是完整的，它的面积就可以直接精确地计算。如长方形的长是 5 c m ，宽是 2 c m 5 × 2 = 1 0 ，一共有10个面积是 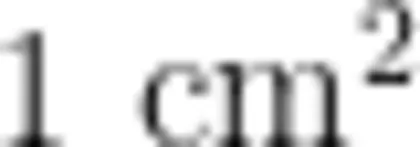的小正方形，它的面积就是 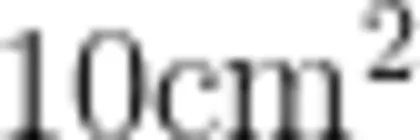。但是像平行四边形这样的多边形，有些边是斜的，所以面积占的方格不全是完整的小正方形，数出的结果往往就不精确了。

【思考】学生借助方格纸计算平行四边形的面积，丰富了面积度量的直观体验。图形中包含一些不完整的面积单位，就增加了数的不确定性。这样的体验，促使学生主动去寻找更简便的数方格的方法。

2.精确度量，再次催生转化的内需

师：同学们，平行四边形的面积就只能这样估算吗？

生：不是的。

生：我们可以想办法把这些不完整的小正方形变成完整的小正方形，然后再精确地数出来。

师：真的可以吗？同学们动手试试看，然后再与同桌交流一下各自的方法。

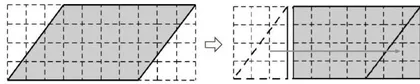
生：我把平行四边形分成了三部分，中间是一个正方形，面积是 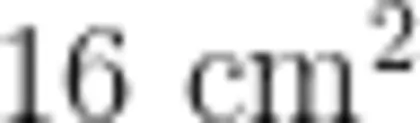，两边是三角形，面积都是小长方形的一半，面积是 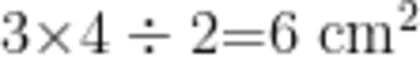，最终平行四边形的面积是 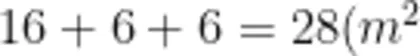（课件展示，如图4所示）。

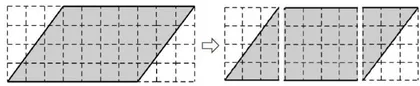
生：我把左边的三角形剪开移到了右边，这样平行四边形的面积就变成了一个长方形的面积，为 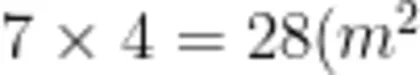（课件展示，如图5所示）。

师：仔细比较两个同学的方法，有什么相同和不同的地方？

生：一个是把平行四边形分成三部分，另一个是把平行四边形分成两部分。

生：它们都是竖着分的，这样刚好可以拼成一个长方形。

师：竖着分其实就是沿着平行四边形的什么 来分呀？

生：高。

生：在计算平行四边形面积的时候，都用到了长方形的面积。

生：原来只能估算的，现在可以精确地计算了。

师：是的！它们都有一个共同的特点，就是当图形中包含一些不完整的面积单位时，我们可以通过改变图形的形状精确地计算它们的面积。比如，把三角形看作半个长方形，或者把平行四边形沿着高剪开，拼接成一个长方形。通过转化再计算，我们发现，这个平行四边形的面积是 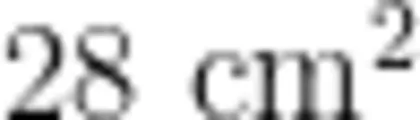。这时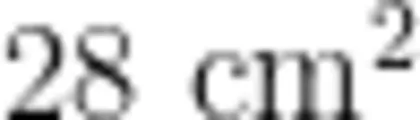的 和刚开始的 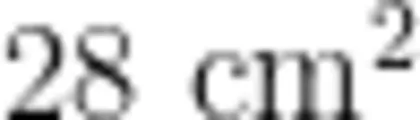一样吗？

生：不一样。

生：刚开始的 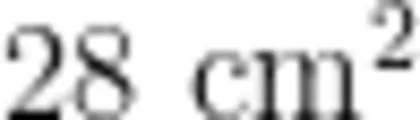是估算的，现在的 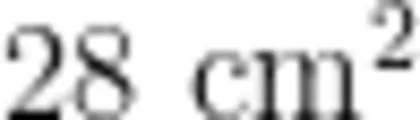是精确计算的。

生：两个都是 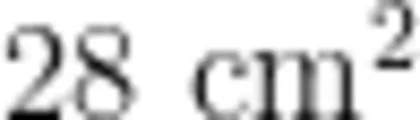，看起来一样，其实只是凑巧而已。换了别的平行四边形，结果可能就不一样了。

【思考】如何让学生深刻理解并感悟面积计算就是将“不完整的面积单位”通过改变图形的形状来实现精确的计数，这是本课教学的重点。在估算的基础上，教师放手让学生去探索。通过比较，学生发现不管用哪种转化方法，都是为了实现从“估着数"到“精确数”，从“一般地数"到“优化着数”，这也是面积度量和转化的本质意义。“两个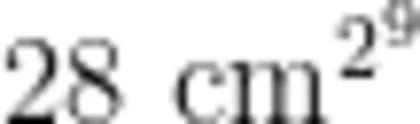 的比较，帮助学生进一步理解面积的意义、增强转化的内需，也为面积公式的生成提供了丰富的认知基础。

三、辨析明理，感悟面积公式的内涵

师：大家分析得很有道理！以后遇到求平行四边形面积的问题，你们会怎样做呢？动手试一试。

（先测量再计算，取整厘米数）

师（呈现学生作品，如图6所示）：仔细观察，你们发现了什么？

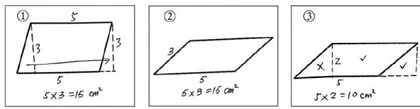
生： ② 和 ③ 算的是同一个平行四边形的面积，但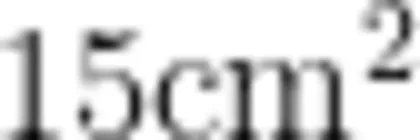一个是 ，一个是 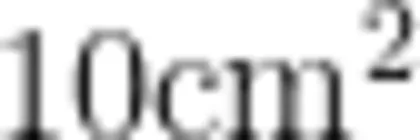，肯定有一个算错了。