把握概念本质，感悟数的一致性

分数教学一直是“数与代数"领域公认的教学重点和难点，在平时的学习中，部分学生对分数意义的理解浮于表面，呈碎片化，没有感悟到整数、小数、分数概念本质上的一致性。老师站在单元整体教学的视角，把握分数的内容结构，抓住分数本质，引导学生逐步把分数知识融人数的学习系统，形成知识网络，从而促进学生的深度学习。

【片段一】立足“一”以贯之，打通知识联系

小学阶段的整数、小数、分数的学习一脉相承，不可分割。整数、小数、分数的产生都和"1"密切相关，人们对整数的认识从“1"开始，对小数、分数的认识也从“1"开始，分数和小数是数的认识的扩充。在平均分物时，所分出的部分无法用自然数表示，为了表述物体中的部分就产生了分数和小数。

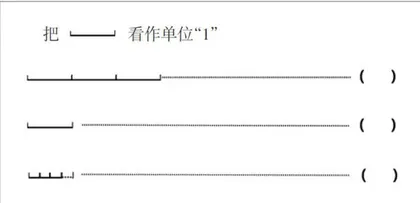
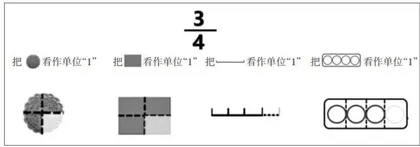
师：如果把一个月饼看作单位“1”，如图1中的这些月饼可以怎么表示？

生：把一个月饼看作单位“1”，4个月饼就用4来表示。

师：图2中的月饼现在可以怎么表示？

生：现在正好是一个单位，就用1来表示。

师：图3呢？

生：用 表示，因为把一个月饼平均分成4份，取其中的3份就是

[教师随后出示3组不同的单位“1"进行巩固练习（如图4）]

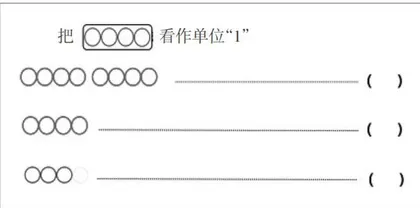
师：刚才我们将1个月饼、1个长方形、1条线段、4个圆分别看作单位“1”，得到了很多的数，仔细观察我们得到的这4组数，你们有什么发现吗？（如图5）

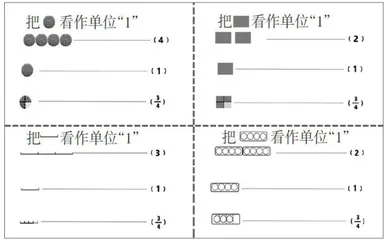
生：都有 ，都有1。

师：为什么有的用整数表示，有的用分数表示呢？

生：有几个单位“1”，就是几；不够单位“1”，就要平均分，用分数表示。

师：是的，把单位“1”累加起来就得到整数，把单位“1”平均分就得到分数。

【赏析】在教学中，郑老师从“1”入手，“1"以贯之，分别从累加和平均分两个角度理解单位“1”，拓展单位“1"的内涵，体会“1"对于整数、分数和小数的价值，沟通整数和分数之间的联系。把单位“1”累加起来得到整数，把单位“1"平均分得到分数，单位“1"就像桥梁，把整数和分数紧紧联系在一起。

【片段二】巧设两次对比，聚焦概念本质

师：如图6，我们把1个月饼、1个长方形、1条线段、4个圆分别看作单位“1”，单位“1”不同，为什么都可以用 来表示？

生：因为它们都是把单位“1”平均分成4份，表示其中的3份，用 来表示。

（教师出示探究任务单：把12个△看作单位“1”，你能创造出一个分数来吗？平均分一分、圈一圈、写一写。学生完成后汇报交流，课件展示，如图7所示）

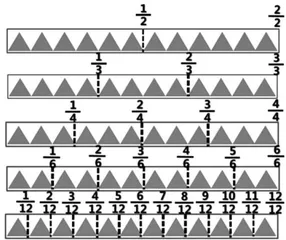
师：同样是把12个△看作单位“1”，为什么可以得到这么多不同的分数？

生：因为平均分的份数不同。

师：即使平均分的份数相同，都平均分成6份，为什么得到的分数也不同呢？

生：因为表示的份数不同。

师：平均分的份数是分母，表示的份数是分子，就像这样，把单位“1”平均分一分，再取一取，分数就产生了。你能用自己的话说一说什么是分数吗？

表示的份数 分子平均分的份数 分母

生：把单位“1”平均分成若干份，表示其中的一份或几份，都可以用分数来表示。

（赏析】在教学中，郑老师设计了两次对比，第一次对比将四个图集中呈现，引发学生思考：为什么单位"1"不同，却都可以用 表示？引导学生通过观察、比较和分析，发现它们之所以都能用 表示，是因为不管把什么看作单位“1”，只要把单位“1"平均分成4份，表示其中的3份，就可以用来表示。第二次对比是学生根据探究要求创造出不同的分数后，提出问题：为什么单位"1"相同，表示相同部分却可以用不同的分数来表示？引导学生发现，虽然单位“1"相同，但是平均分的份数不同，表示的份数也不同，所以即使表示相同的部分用到的分数也不相同。在两次对比中，学生进一步感受分数的产生不仅要关注单位“1”，也要关注平均分的份数和表示的份数，加深了学生对分数本质的理解，有效发展了学生的数学抽象能力。

【片段三】沟通三者联系，感悟数的一致性

《义务教育数学课程标准（2022年版）》指出，数的认识教学，要让学生“初步体会数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识”。分数、整数、小数都是对计数单位和计数单位个数的表达，它们之间存在很多联系，整数以“1"为计数基础，每增加"1"就形成一个新的数。把"1"平均分成若干份，创造出了分数的计数单位，再数分数单位的个数，得到不同的分数。将"1"细分得到小数单位，小数单位累加就可以得到小数。正是它们存在这样的一致性，所以，在教学中，教师要突出“计数单位"这个核心概念，让学生整体上建立整数、小数和分数在表达方式上的联系，加深对分数意义的理解，感悟数概念在本质上的一致性。

师：刚才我们认识了分数，知道了把单位“1”平均分成若干份，表示这样一份或几份的数，叫作分数。想一想，为什么要突出这样的一份呢？再回到刚才得到的分数中，你能找到表示这样的一份的数吗？

（预设：学生可能会想到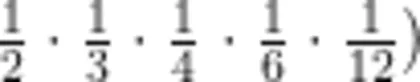

师：把单位“1”平均分成若干份，表示其中的一份的数，我们把它们看作分数的计数单位，就像整数的个、十、百、千，也像小数的十分之一、百分之一、千分之一，我们把它叫作分数单位。仔细观察这些分数单位（如图8），你们有什么发现？

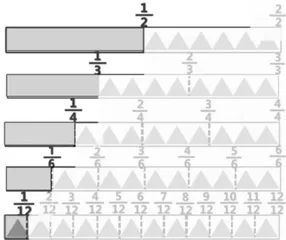
生：分数越来越小。

师：为什么会越来越小？

生：因为平均分的份数越来越多。

师：同学们，你们觉得是什么决定了分数单位的大小？

生：分母，平均分的份数。

师：分子又表示什么呢？ （20 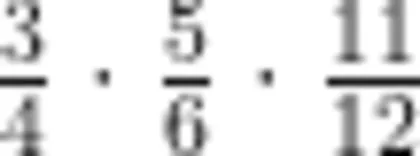分别有几

个分数单位？

师：你们怎么一下子就说出了它们有几个这样的分数单位？你们看的是什么？

生：分子，分子表示分数单位的个数。表示的份数 ·分子… ·分数单位的个数平均分的份数… …分母··分数单位的大小

师：认识了分数单位，我们再来看分数的意义，在概括分数的意义时，我们将分数概括为“表示这样一份或几份的数”。现在，你们知道为什么要突出这一份了吗？

生：“一份”很重要，它是分数单位，分数都是由分数单位相加得到的。

师：比较一下，整数、小数和分数在表达方式上有什么相同的地方？

生：分数与整数、小数一样，都是由若干个计数单位相加得到的。

【赏析】在教学中，郑老师从分数的意义的定义入手，引导学生思考“一份”的重要性，让学生在观察、分析和比较的基础上，找到分数与分数单位之间的关系，并将分数单位与分数的意义建立联系，突出“一份”的重要性，深化对分数意义的理解。同时，郑老师引导学生找到整数、小数、分数之间的联系，感受由“计数单位”的累加得到不同的数的过程，体会“计数单位"对理解整数、小数、分数概念的价值，感受数概念在本质上的一致性。

总之，郑老师立足单元整体教学视角，把握数学知识的本质，建立知识的前后联系，帮助学生建立结构化知识体系，改变课时单一的教学视角，基于单元又超越单元，有效实施大单元教学，促进学生的深度学习，发展学生的数学核心素养。

（作者单位：山东省胶州市向阳小学山东省青岛市西海岸新区教育和体育科学研究院）