立足竖式功能，依托数学文化，促进意义建构

竖式就是把需要计算的数和运算符号按规定的格式写出，再按运算法则进行计算，并把计算的中间过程与最后结果记录下来。竖式是在最大程度压缩步骤和尽可能保留过程的需求中寻求平衡的结果。笔者通过对除数运算历史的追溯和对运算一致性的理解，构建了从减法运算引入、用除法运算意义和乘法运算支持的除法竖式教学的“新路径”。在教学中，教师要厘清除法竖式的来龙去脉，引领学生经历同数连减的减法竖式迭代为除法竖式的过程，促进学生对除法竖式的意义建构，突破学习难点。

一、解读史料，寻找除法竖式的“源”

历史是教学的指南，在遇到教学疑难问题时，我们可以尝试寻求历史的“帮助”。为了使除法竖式学习更有意义，突破学习难点，我们可以对除法竖式的历史进行追溯。历史上除法算法众多，以用罗马数字竖式书写的 2 1 ÷ 7 = 3 和18世纪前后欧洲出现的用减法计算的‘ 1 5 5 4 ÷ 3 7 = 4 2 竖式为例（如图1）。计算 2 1 ÷ 7 ”就是求21可以减去几个7，计算" 1 5 5 4 ÷ 3 7 ”就是求1554可以减去几个37。

X X I ÷ V I I = I I 1554 249759701 S7 L.VⅡI 118XV I.VⅡIII1.VIIVⅡ IV.

罗马数字书写的竖式 欧洲用减法计算除法

从上述两个例子可以看出，除法运算实际上来源于减法，其本质是从被除数中逐次减去除数的倍数，最后将减去的次数统计出来就是除法的结果，记录整个过程，便是除法的竖式。

清代康熙皇帝亲自主持编写的《御制数理精蕴》一书，记载着用乘法竖式的写法来计算除法的竖式。图2就是书中记载的 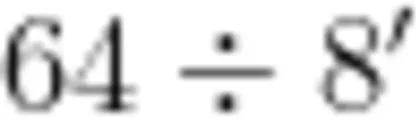的计算过程和用现在的语言分步进行解释的过程。

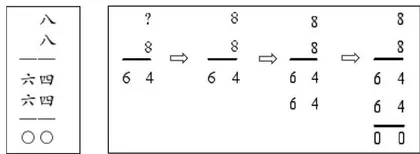
从图2中可以发现，《御制数理精蕴》中计算除法的思维方式、计算过程与现代教科书上的除法竖式基本一致，整个过程就是运用乘法计算除法，相当于“8乘几等于64”，按照“商一乘一减"三步完成了整个除法竖式的计算过程，将这个竖式中的除数“8”移出来写到左侧，记录方式就与现在教科书上除法竖式的写法基本一致。

数学史在“教什么”的问题上帮助我们达到了正本清源的目的，在“怎么教”的问题上启发我们返璞归真，回归数学的本源。除法与减法、乘法运算的关系在《义务教育数学课程标准（2022年版）》提出的运算一致性中得到了进一步诠释。加法是所有运算的基础，其他运算都是通过加法运算衍生而来的，减法是加法的逆运算，乘法是同数连加的简便运算，除法既是乘法的逆运算，又是同数连减的简便运算。由此可见，从除法运算的历史出发教学除法竖式，可以有两条路径，第一条路径是建立除法与减法的关系，从减法竖式中引出除法竖式；第二条路径是明晰除法与乘法的关系，从乘法竖式中引出除法竖式。

二、实施除法竖式教学的新路径

（一）从分开始，提炼除法问题的五要素

除法是同数连减的简便计算，设想在教学开始就退到知识的原点。教师出示人教版小学数学教材一年级下册“100以内的加法和减法（一）”的同数连减解决问题：28个橘子，9个装满一袋。让学生思考：分掉了几袋？已经分走几个橘子？会有剩余吗？学生通过圈一圈，列出了两种算式（如图3）。

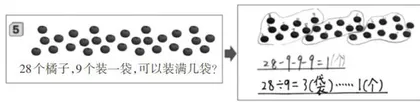
首先，教师引导学生对照图示理解两种算式的含义，并从图示和算式中提炼出除法问题的五要素：分的总数、每份分多少、分成几份、已经分掉了几个、还剩几个。

接着，进行连减横式和除法横式的比较，让学生感受除法和减法的关联，结合情境意义理解横式中每个数字在图示中的意义。对照五要素，发现两个横式都只反映了其中的四要素，都没有记录“已经分掉的个数”这个要素。

最后，引导学生在不同的横式记录和图示中找到“已经分掉的个数”，将减法、除法分别与乘法建立联系，为后续创造除法竖式提供有力支撑。

（二）巧借连减竖式，创造能记录五要素的除法竖式

教师通过三个关键活动，让学生经历除法竖式的生成与创造的过程，感悟能记录五要素的除法竖式的合理性和简洁性。

1.独立尝试，用竖式记录分橘子的过程

学生尝试用竖式记录分橘子的过程，往往通过已有加减法竖式的表象迁移，创造出如图4所示的竖式。尽管这个结果与标准的竖式差距较大，但通过这个活动，可以了解学生思维的起始状态，为创造标准的除法竖式提供了思维碰撞的原始素材。

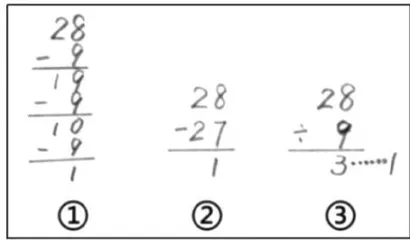
2.评价分析，用除法问题的五要素审视竖式

在这个环节中，教师引导学生积极参与，对照除法问题的五要素对上述三个竖式进行分析。竖式 ① 按照分橘子的活动，用“连减竖式"表示了从28个橘子每次取了9个，取了3次，还剩1个，契合连减的横式。竖式 ② 能表示28个橘子取走了27个，还剩1个，但是不能反映这27个是如何取走的。竖式 ③ 把除法横式从上往下列，记录了除法问题的四要素：分的总数、每份分多少、分成几份和还剩几个。但是没有反映“已经分掉的个数"和“剩余个数的由来”。整个过程围绕着除法问题的“五要素”，将评价的视角聚焦到完整、清楚地记录分的过程，即关注除法竖式的内在结构。

3.取长补短，借助分的过程建构除法竖式

通过分析，我们发现上述三个竖式都无法同时记录除法问题的“五要素”，那么这三个竖式之间有没有内在的联系呢？如果在这些竖式上添加缺少的要素，又该怎么改造呢？尽管学生不可能在短时间里真正创造出标准的竖式，但这样的经历却是宝贵的。如图5所示，因为求简的需要，竖式 ① 可以直接简化、压缩成竖式 ② ，只要在竖式 ② 的基础上记录“每袋分9个"和“分了3袋"这两个要素，整个竖式就能完整记录除法问题的五要素。通过连减竖式改造生成除法竖式，学生经历了除法竖式的形成、演变历程，使除数竖式复杂的表象背后所蕴含的多维关系结构得以显现，促进了学生对除法竖式结构的理解，让学生能感受除法竖式的完整性和简洁性。

（三）多元表征关联，促进除法竖式的意义建构

为了帮助学生更好地理解除法竖式的意义，

并掌握书写顺序，在创造除法竖式后，要及时将竖式与多元表征关联。

1.将除法竖式书写过程与具体的操作活动关 联

计算的过程就是一种逻辑推理的过程，学生在算理的学习中，借助动作表征经历逻辑推理的过程，从而形成计算思维。在得出除法竖式后，教师要引导学生将除法竖式规范的书写顺序与分物的过程联系起来，知道“9）28"表示"28个橘子，每9个装一袋”，可以装满3袋，所以商是“3”；乘法口诀“三九二十七"求出了“每袋装9个，装满3袋分走了27个”，竖式中的“27"表示“已经分掉的个数”；知道了“一共有28个橘子，已经分掉了27个，还剩余1个”，所以横线下面写上"1”。整个过程将分物操作与除法竖式有机结合，将直观表达与抽象思维相互转换，促进了学生对除法竖式的结构和运算过程的内化理解。

2.将除法竖式与除法横式关联

对于学生来说，除法横式是旧知识，除法竖式是新知识，教师要将除法竖式中的各部分与横式的各部分一一对应起来，不仅记录了“已经分掉的个数”这一重要元素，还清楚地记录了“从总数里减去分掉的个数等于余下的个数"这一思维过程，能帮助学生理解除法竖式记录的合理性和完整性，从而更好地理解除法的运算过程。

3.将除法竖式与除法意义关联除法的本质是不断地对不同单位的总数进行平分的过程，分了之后对剩余部分进行转化，与下面的单位进行合并，再重复这样的过程。这也解释了为什么除法竖式和其他三种竖式的计算形式不一样，因为加法、减法和乘法都只涉及参与计算的两个数以及运算结果，但除法还要涉及余数以及对余数的转化处理。因此，必须采取这种可以连续进行记录的方式。在除法竖式的“引出”阶段，学生无法体验对剩余部分继续转化为较小单位继续平分的需要，所以学生对在竖式中记录“已经分掉的个数”的必要性体验不深，但可以通过除法竖式解释除法问题的五要素，借助除法竖式结合问题情境解释除法等分除或包含除的意义，能进一步理解除法、商和余数等概念，以及余数与除数的关系，从而深化对有余数除法意义的理解。

综上所述，教师要基于对除法运算历史的追溯和对运算一致性的理解，将除法竖式教学根植于“减法运算"的沃土中，从运算意义出发提炼出除法问题需记录的五要素。教师要鼓励学生从自己的认知出发，创造自己能够理解的竖式来记录除法运算的计算过程，通过筛选、简化、改造，立足竖式的记录功能，形成除法竖式的“结构”，进而通过多元表征联结，提炼出除法竖式模型。整个学习过程，学生经历了将同数连减的减法竖式迭代为除法竖式的过程，厘清了除法竖式的来龙去脉，感受到其与减法竖式内在的一致性，促进了对除法竖式的意义建构。

（作者单位：浙江省杭州市临平区文正小学）