浅谈小学数学结构化教学的三个转化

《义务教育数学课程标准（2022年版）》（以下简称新课标）在教学建议中提出：“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。”回观当前的数学教学，依然存在教师目光短视的问题，对学生的学习缺乏整体观念，只看到当前，满足于本节课的情境或活动设计，忽略了学生数学思维和能力的培养。下面试从“教什么”“怎么教”“教到哪”三个维度谈谈个人的探索与实践。

一、整合结构，化“碎”为“整”，厘清知识网络

美国心理学家布鲁纳最早提出学习知识结构，他认为，学习结构就是学习事物是怎样相互联系的。数学知识本身具有很强的内在逻辑，是整体的、系统的、结构的。知识点不是孤立零散的碎片，而是一个庞大的纵横交错的结构网络。在教学中，教师不仅要引导学生理解和应用知识，还要帮助学生形成知识结构，掌握数学知识的本质特征和相互联系。

如，教学“表内乘法和表内除法（二）”复习课时，是在学生已学完1～9的乘法口诀和乘法口诀表的基础上教学的。

师：根据“三五十五”这句口诀，你能想到哪些算式？先想一想，再打开学习单填一填。

师：说说看，这些算式为什么都跟“三五十五”有关？看来乘法口诀不仅能解决乘法问题，还能解决加、减、除法问题啊！

师：这些算式都用到了同一句口诀，大胆想一想，你觉得加、减、乘、除之间有关系吗？比如乘法和除法….

生1：我觉得乘法和除法间有关系，乘法的积就是除法的被除数，乘数分别是除法的除数和商。

生2：乘法是求3个5的和，除法是反过来把15平均分成3个5。

师：说得真好。那我们就可以说乘、除法之间是—相反的。

生：我觉得乘法和加法也有关系。因为这里的加法表示3个5相加是15，乘法也是这个意思。

师：那加法和乘法都表示同样的意思，有加法就可以了，干吗还要学乘法？

生1：因为不是所有的加法都能改成乘法。

生2：因为乘法是加法的简便运算。

师：是的。看来加法和乘法之间关系密切，可以说它们的关系是—相近的。

生：加法表示3个5相加等于15，减法表示15减去3个5等于0。可以看出来加减之间的关系也是相反的。

师：同学们真厉害，那减法和除法间呢？好像没有什么关系了吧？

生：不对不对，减法是15不断减去5，一直减了3个5，最后等于0，可以看出15里面有3个5。除法也表示15里面有3个5，意思一样。

生：虽然它们表示的意思一样，但除法更简便。我觉得减法与除法之间也是相近的。

师：同学们太了不起了！原来加、减、乘、除之间是相通的。

二、回归本质，化“浅”为“深”，培养核心素养

新课标指出：“要强化对数学本质的理解，关注数学概念的现实背景，引导学生从数学概念、原理及法则之间的联系出发，建立起有意义的知识结构。”学生要建立有意义的知识结构，需要对学习经验不断进行重组和优化。学习经验的获得，需要教师精心设计课堂教学，帮助学生深度理解数学知识的本质，引导学生经历知识结构的生成过程，让这些“经历"沉淀为“经验”，再由“经验”走向“建构”，促进结构性思维从外到内得到发展。

如，“认识厘米”是“厘米和米”的起始课。在本课开始建立适合学生的学习结构，能为后续学习别的度量单位形成量感提供经验的迁移。任何的度量，都离不开“度量单位”“度量对象”和“度量结果”三要素。而度量的本质，就是度量单位的叠加。在教学中，不能满足于双基的落实，要立足度量的本质，引导学生看到度量对象时，第一反应就是看里头包含多少个度量单位。

【教学片段】

在学生认识了“1厘米”有多长，建立初步的表象后。

1.加深体验，强化对1厘米的感知。

体验1：直尺上相邻两个数字间的长度都是1厘米，用手在尺子上比画出1厘米有多长，拿开尺子，仔细观察1厘米的长度，牢牢记在心上。

体验2：找找看，1厘米还藏在我们身边哪里？

体验3：看，老师带来了好多把尺子，你觉得你直尺上的1厘米，和老师这把米尺上的1厘米，和这卷尺上的1厘米比较，哪种尺子的1厘米长，还是一样长？

2.运用变式，领悟度量的本质。

变式1：学具盒里的这只彩色笔有多长，不用尺子，你能量出它的长度吗？

变式2：

师：小芳用这把尺子量出钉子的长度是8厘米，你同意吗？为什么？

追问：为什么我们可以用“8-2”来计算钉子的长度？

变式3：

师：你能用下面这把尺子画出几种不同长度的线段？

三、立足整体，化“近”为“远”，打好学习通路

小学数学单元整体教学，除了自然单元内的内容重组，还包括整体视角下的内容重组。也就是分析教材中的自然单元，将有内在知识联系的单元作为整体，教学时要以所学内容的核心概念为统领，建立知识间的关联，促进知识与方法的迁移，发展学生的核心素养。

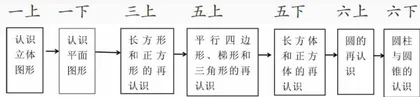
如，一年级下册“图形的认识”，本节课在教材中什么位置？要学习什么内容？哪些内容与这节课有关？教师要做到心中有数，理清知识结构图，做到既见树木，又见森林。在教学时，还要重视纵向拉伸，将单元内、单元间，甚至跨年级的同类知识按其内在逻辑组成由简单到复杂的结构链，凸显背后共通的思维方式，使知识和学法辐射得更远。

【教学片段】

活动一：由“体”到“面”，认识平面图形。

师出示四种立体图形，复习名称并贴在黑板上。

先出示圆形，问：这是什么图形？它是从哪个立体图形上来的？你能上来指一指吗？

生上来把平面图形放到立体图形相应位置进行比对。

再出示正方形，当学生找到正方体的一个面时师追问：还可以从哪里来？

接着出示3个不同的长方形，问：这三个面是从一个立体图形中来的，你知道是哪个立体图形吗？

师再出示一个来自圆柱侧面的长方形，问：加大难度，看谁能找到它从哪里来？

生上来比对后，发现这些立体图形每个平面上的图形都跟这个不同，于是在圆柱侧面绕一圈，找到这个长方形。

最后再认识三角形和平行四边形....

活动二：强化对1平方分米、1平方厘米的感知。

出示1平方分米的正方形，问：这个图形来自哪里？它不在这些立体图形中，在我们身边或者家里找找看。

再出示1平方厘米，问：看看，这么小的一个正方形，它来自哪里？

活动三：给图形分类并命名。

1.猜猜数学家会怎么分？

2.夸夸哪个名字取得好？

3.猜猜我是谁？

先蒙住图形，再慢慢露出来，让学生猜图形。

4.师说图形名称，生比画出图形的样子。

本节课属于“图形的认识与测量”主题，核心概念是维度、图形的特征和度量单位等。立体图形是三维的，平面图形是二维的，“活动一”的设计，让学生直观感受到“面”来自“体”，沟通了三维与二维的联系，发展了空间观念。

总之，小学数学结构化教学就是要将知识结构与学生认知结构融入情境中，引导学生观察、体验、思考、感悟，提升学生的自主建构能力，促进知识结构化生长，发展学生的核心素养。