数学之美 文化之韵

平均数是人教版数学四年级下册第八单元“平均数与条形统计图”的一个内容。从小学阶段整个知识体系来看，“平均数”属于“统计与概率”领域的内容，也是小学数学教学中渗透统计思想的主要体现之一，这一学段的目标是理解平均数的意义、会用平均数解决问题，形成初步的“数据意识”。本文依据《义务教育数学课程标准（2022年版）》中“继承和弘扬中华优秀传统文化”，定位从统计学的角度，结合我国古代数学著作《九章算术》“方田章”中的内容入手来教学和理解平均数，通过对平均数的特点的探索，将平均数的知识应用到解决问题中，依据学生已有的认知基础实现从统计概念的角度理解平均数的意义，感受数学知识与中华优秀传统文化相融合的魅力。

一、说平均数的意义

平均数是代表一组数据的整体水平，它不同于原始数据中的每一个数据，与每一个原始数据相关，但是又不是任何一个真实的数据。要对两组数据的整体水平进行比较，就可以比较这两组数据的平均数，因为平均数具有良好的代表性，不仅便于比较，而且公平。在本节课导人部分的问题——每人投10个球的投篮挑战赛，简单且易于引发学生对平均数的“代表性”的思考：是用一个人投篮投中的最多个数还是最少个数来代表整体水平，还是用几人投篮的总数来代表整体水平呢？或是找到某一个数来代表整体水平呢？

教学片段：

师：最近我们学校的篮球赛正在如火如茶地进行中，为了组建最强战队，我们班的男生和女生开展了投篮挑战赛，规则—每人投10次。一起来看看他们的比赛结果：从这两幅条形图里，你知道了哪些数学信息？

出示下图：

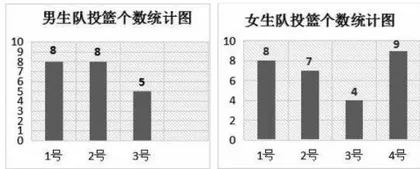
生1：我知道了男生队有3人，分别投了8、8、7个，女生队有4人，分别投了8、7、4、9个。

师：你发现了每个人实际投球的个数，还有补充吗？

生2：男生队一共投了21个，女生队一共投了28个，女生 投球数更多。

师：你知道了总个数，那根据这些信息比一比，哪一队更厉害？为什么？

师：为什么不能比较两队的总数？

生3：因为人数不同。

师：孩子们，你们真善于观察，人数不相等的情况下我们来比较两队的总个数公平吗？是啊，不公平，那我们把两队成绩最好的挑出来比一比，男生队8个，女生队9个，女生队更厉害，你认为这种比法怎么样？

生4：一个人不能代表一个队。

师：你说得特别有道理，一个人的成绩不能代表一个团队的整体成绩，那到底哪个数才能代表一个队的整体水平呢？

生5：平均数。

二、说平均数的特点

区间性，根据投篮的例题，平均数说了他在最大最小数之间；通过一个小程序，平均数说了他的敏感性，会受较大或较小数的影响。男生队的平均数有时会出现小数，而小数不能用来代表男生投篮的具体个数，从而感知平均数的虚拟性。

教学片段：

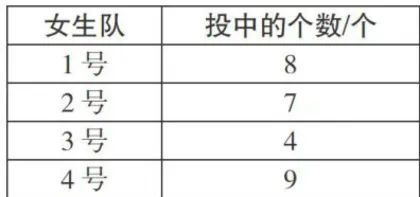
师：不计算，估一估这组数据的平均数是多少？生1：我估计是6。

生2：我估7。

师：为什么不估4？为什么不估9？

生3：因为4太小了，9太大了。

师：说得太好了，9是这组数据中的最大数，4是这组数据中的最小数，所以不能估。计算验证一下。

小结：这样看来，平均数在这组数据的最大数和最小数之间，它是有一定的区间范围的。通过探究，你们又发现

教学纵横

了平均数的区间性。

师：真是难不倒你们啊，现在结束了第一轮比赛，你发现了什么？

生：两个队的平均数相同，不知道谁厉害。

师：是的，没有分出胜负，我们班的男生跟你们一样敢于挑战，不服气，想比一次。于是派出了4号男生出征，你们猜猜4号男生会投中几个？

生1：投中10个。

师：看来你认为4号男生很厉害，如果投中10个，平均数会不会变？怎么变？

生2：平均数会变大。（Excel演示平均数的变化）

师：再猜一猜还可能投中几个？生3：7个。

师：那此时平均数又会怎么变化？假如4号男生只投了1个呢？

生：如果是7，平均数不变。只投1个，平均数会变小。

师：根据刚才的过程，说说你的感受。

生：平均数会随着其中一个人的数变大或变小。如果增加的数字很大，它就会变大；如果增加的数字很小，它也会被拉低。

师：没错，孩子们，平均数好善变啊，从它的善变中我们能感受到它十分敏感。这体现他的敏感性。除此以外，你还有什么发现？

生：我发现有时平均数是一个小数，这不可能。投球个数不会是小数。

师：你太会思考了，平均数是我们为了匀一匀而创造出的一个虚拟的数。所以他还具有虚拟性。

三、说平均数的计算模型

移多补少的操作模型和求和均分的计算模型。学生通过自主探究发现了两种求平均数的方法。先通过画图体会移多补少的过程，再利用教具展示，进一步感受匀一匀后找到一个相同的数就是这组数据的平均数。但是遇到更大的数据时，移多补少还方便吗？那就采用求和均分的方法。

教学片段：

活动：感知平均数，形成表象。

学习任务：1．用你喜欢的方式找到一个能表示男生队投球水平的数。（画一画、移一移或算一算）

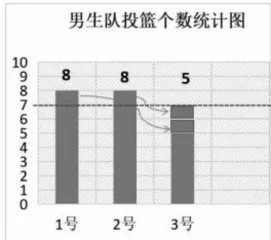
2.和同桌说一说你的想法。

生1汇报：

方法1：移一移，把8里的1给5，第二个8的1也给5，三次都是7，所以男生队平均每次投中了7个。

师：为什么要这样移来移去？

生：我想使得每份同样多。

师：在移动过程中，什么没变？

生：总数没有变，人数也没变。

师：那什么变了？

生：每份的个数变了。

师：没错，像这样在小组内部成员之间匀一匀平衡一下，看上去每份都同样多。将一组数据中多的移给少的，你给这个方法取个名字。

生：拆东墙补西墙。

师：生活中可以这么理解，在数学上我们叫移多补少。

师：请问在计算男生队平均投球数时，除了移多补少，你还有什么方法？

方法2： （8+8+5）÷3=7 （个）。

师：你是怎么想的？为什么要除以3？

小结：先求总数，再除以份数的方法叫作先总再分。7就是8、8、5的平均数。

四、说平均数的统计价值

平均数的统计意识，通过分析做出决策。生活中的平均数，如美团美食评分、携程旅行酒店评分、景点评分等都可以为我们提供参考。电影评分对观众选择的影响和引导，让学生在应用中感受平均数的比较性价值和预测性价值。同时，我们也要让学生知道平均数给出的是一个评价标准，并不是做出判断和决策的唯一标准，以此培养学生的思辨能力。

教学片段：

师：生活中还有许多平均数，我们一起看一看。根据这些平均数你知道了什么？

生：根据这些评分我们可以参考着选择想看的书籍、电影，出去旅游时也为我们提供了许多参考意见。

师：是的，孩子们，生活中的平均数是无处不在的。

五、说平均数中的中华优秀传统文化

《九章算术》作为中华文明的瑰宝，是古代数学家智慧的结晶，也是中华民族优秀传统文化的重要组成部分。《九章算术》“方田章”中的数学问题涉及分数的计算与比较，以及通过“减多益少”等方法实现平均分配，这为学生提供了学习平均数概念的实例和途径，课堂教学中教师再现古代对“平分术”问题探索的过程，有助于学生理解平均数的概念和计算方法，同时培养逻辑思维和问题解决能力，有助于增强文化自信，传承和弘扬中华优秀传统文化。

教学片段：

师：通过巧妙地移多补少的方法，我们顺利地找到了男生队的平均投球个数，其实早在很多年前，我国的九章算术中就已经提到过这种方法，谁能模仿着古人的语气为我们读一读这段文字？

生：“方田章”：今有三分之一，三分之二，四分之三。问：减多益少，各几何而平？

师：读得太有感情了，同学们都读懂了吗？这是什么意思？配着动图仔细观察，现在看懂用了什么方法了吗？

生：减多益少就是移多补少。

师：没错，减多益少就是移多补少，看来我们和古人想到一块去了。虽然这里匀的是分数，但思想是一样的。

结语：

平均数一课的教学改以往“纯”数学味为“重”数学味，且“融入”中华优秀传统的文化味，让平均数通过“说话”，将整节课的教学内容和思路展示出来。

中华优秀文化融人数学教学并不是简单的一个历史故事引人、一段史料的介绍，而是我们在教学数学知识的过程中将古代探索知识的情境再现，通过体验古代数学家探索知识的过程，对话和模仿古人解决问题的思维模式，使学生在数学学习的过程中感受古代数学家的智慧，增强文化自信和民族自豪感，做我国优秀传统文化的传承者。

【注：本文系昆明市教育科学规划课题“中华优秀传统文化融入小学数学教学的实践研究”（项目编号：JG2024007）阶段性成果】