高等数学课程教学中存在的问题及对策研究

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2025）14-0108-06

Abstract：Amongallcoursesoferedincollgesanduniversities，Higher Mathematicsoccupiesthecore position.Itisnotonly thebasisforleamingfollowupmathematicscouses，butalsotheprerequisiteforlearningnumerousprofesionalcoursesIisnot onlyadegreecourse，butalsooneofthecompulsorysubjectsinthelarge-scaleexaminationsthatarecloselyrelatedtothefuture ofthecandidates，suchashighereducationexamination，postgraduateentranceexamination，civilservantexaminationandmilitary civilianexaminationBecauseofthis，theteachingqualityofHigherMathematicsnotonlyafectsthetrainingqualityofprofesional talentsincolegesanduniversities，butalsoafectsteighereducationadmisionrate，thegrduateschooletranceeamination rateandthegraduateshoolentranceexaminationrate，andthesedatawilleventuallyafectthecomprehensiverankingofcoleges anduniversties.InordertoimprovetheteachingqualityofHigherMathematics，thispaperanalyzesthemainproblemsexistingin theteachingprocessandasessmentofthiscourseinouruniversityindetailandgivessometargetedmethodstosolvethe problems.These methods can be used for reference for other universities facing the same problems.

KeyWords： Higher Mathematics; teaching quality; teaching problems; teaching strategy; course assessment

高等数学是高校理工科、经管类、医学类各专业必修的公共基础课程之一，是从社会需求和人才培养的角度出发而开设的一门通识教育基础理论课程。该课程既是学生就业、创业、深造的奠基石，又是终身教育的重要组成部分，只有学好了这门课程，才能顺利地进入到各门专业课程的学习中。从知识层面讲，该课程的理论知识在诸如计算机、软件开发、电子科技、电气工程、建筑行业、军事、生物医学、天文学和财经等领域均有广泛应用。从能力层面讲，学习数学并不是简单的学习计算方法，而是锻炼思维、提升能力的过程，该课程可以培养学生的逻辑思维和推理能力，探索精神和创新能力，以及发现问题、分析问题、解决问题的能力。高等数学课程该如何教、如何学，才能达到较好的教学效果和学习效率，是教师们一直关注和探索的问题，虽然目前已有众多学者从理论层面给出了多种提高高等数学课程教学质量的策略，但教学问题既带有共性又具有个性，同一门课程在社会发展的不同时期、面对不同的授课对象时，总会出现一些新的问题，要解决这些问题，必须关注授课对象自身的特点，以学定教、顺学而导。本文首先详细分析东华理工大学高等数学课程教学中存在的一些问题，然后给出解决这些问题的有针对性的建议。

一 主要存在的教学问题

在本课程的教学过程与考核评价中，主要存在以下问题：

（一）教师的"教"缺乏必要的约束与规范

作为一所理工科院校，东华理工大学（以下简称"我校”除了文学、法学、艺术、体育和英语几个专业以外，其他专业都开设了高等数学课程。根据专业需求的不同，我校的高等数学课程分成了A、B、C、D四个批次，不同批次有不同的教学要求，并根据教学要求的不同制定了不同的教学大纲，同时期末考试也分批次单独命题，试题的范围和难度各不相同。

从教学规范的角度来讲，教师的教学应该严格依据教学大纲展开，根据教学大纲中规定的教学内容的广度和深度，合理安排授课内容、授课进度，并选择相适应的授课方式。然而实际上，由于师资紧张，我校的数学教师会同时承担不同批次的高等数学课程的教学，因为采用的教材相同，所以当同一位教师为不同批次、不同专业的学生讲授该课程时，习惯上采用相同的教学内容、教学方法进行授课，完全忽视了教学大纲中的具体要求。而学生作为授课的对象，往往并不知道教学大纲的存在，这就导致即使教师并没有严格按照教学大纲中的教学要求进行授课，学生也浑然不知。也就是说，因为缺少必要的约束与监督，教师的教学内容不一定是规范的；又因为掌握了绝对的主动权，所以在施教过程中，教师极易产生主观性、随意性，最终导致教学过程与教学目标偏离。

（二）学生的"学"缺乏明确的目标和引导

对于绝大部分学生而言，在大学一年级期间时间投入最多的课程就是高等数学，这不仅是因为学生深知这门课程的重要性，而且还因为学生普遍感觉该课程比较难学。客观来看，高等数学课程涵盖的知识点非常多，而且各个知识点之间联系紧密、环环相扣、相互渗透，如果某个知识点未理解透彻，将直接影响后续内容的学习。大学课程的教学节奏普遍比较快，高等数学课程的教学进度更是紧锣密鼓，导致在课堂上很多同学都是似懂非懂的状态，很难完全吃透。因此，要想学好这门课程，仅仅依靠教师在课堂上的“教"是不现实的，学生必须要学会在课堂以外的时间如何自己“学”，如何充分运用课余时间进行有效的课前预习和课后复习，从而对课堂教学进行有益补充。

从目前的情况来看，大部分学生都有学好这门课程的意愿，并且愿意在这门课程上花时间。然而，由于刚刚步入大学不久，很多学生还未适应大学的教学方式，依然延续着高中的学习习惯和学习方法，不擅长进行独立、自由、自主的学习，而是希望被老师牵着鼻子走。另外，由于不了解课程的教学目标和要求，大部分学生不知道哪些是重点知识和关键技能，从而很容易钻到某个其实并不太重要的点上，导致没有将有限的时间和精力花在刀刃上，最终的结果是收获与付出不成正比。

（三） 课时缩减而教学内容和要求却增加

大学是培养人才、锻炼人才的地方，据了解，我国目前大约有 80% 的大学实行学分制度，以此来考察大学生的能力。在学分制的背景下，大学的课程门类在不断增加，而课程学时则持续缩减。以我校的高等数学B批课程为例，该课程教材分为上、下两册，安排在大学一年级的上、下两个学期学完，笔者从2007年开始承担该课程的教学，至今经历了该课程课时的5次调整，按照时间顺序，分别是 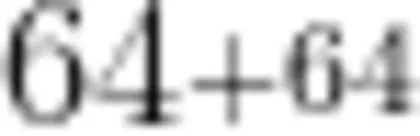，总学时从最初的180学时缩减至150学时、144学时，再缩减至目前的128学时，相较于最初的学时安排，目前的课时缩减率为 28.89% 。然而，值得一提的是，虽然总课时在不断缩减，但教学大纲中对该课程教学内容的广度和深度方面的要求却均未降低，而且期末考试试题的整体难度也一直保持在相同水平。从第一学期的单课时来看，其经历过从90到84再到80的削减过程，而教学内容却从讲完第六章到讲完第七章第四节再到讲完第七章全部（一共有八节）的增加过程，所以可以说，课时的缩减并没有带来对课程广度和深度上要求的降低，相反在某些方面还有所增加。

课时的压缩使本来就不宽裕的课时显得更加紧张，因此为了保证教学进度，很多知识点都无法在课堂上展开讲解，出现了对于教师而言“心有余而时不足”的现象；而且因为要赶进度，所以课堂教学几乎都是教师一个人的独角戏，教师和学生、学生与学生之间缺乏必要的交流与互动，教师过于主动，学生过于被动。

（四） 高中教材过早涉及大学数学知识

现行的高中数学教材包含了一部分大学数学的知识，例如数列与函数极限的计算、基本函数的求导公式、借助导数符号判断函数的单调性、借助导数求极限等，这些内容都是高等数学课程中的核心知识。高中在给出这些知识的时候，通常介绍比较浅显、片面，而且给出的大部分结论是在特定条件下简化的结果。例如：关于数列的极限，高中介绍的方法是通过观察数列的项的变化趋势来得到极限结果，但如果数列通项的表达式比较复杂，该方法则不再适用；关于函数的极限，高中介绍的方法是直接计算函数在相应点的函数值来得到极限值，但如果函数在相应点没有定义，或者极限过程是自变量趋于无穷大，则该方法无法使用；关于函数的求导公式，高中只给出了幂函数、指数函数、对数函数、正弦函数和余弦函数的求导结果，而基本初等函数除了上面提到的这些函数以外，还有正切、余切、正割、余割函数，以及反三角函数，这些函数的求导，高中并未介绍；关于函数的单调性，高中只给出了在函数可导的前提下判断单调性的方法，并且学生普遍熟记“极值点处的导数必为零”这一结论，但实际上，如果去掉可导的前提条件，该结论实际上是错误的；关于运用导数求极限的洛必达法则，高中只介绍该方法如何使用，却未介绍该方法的适用对象，以及使用该方法时的一些注意事项，很多学生误以为该方法是万能的，所以经常过度使用。

高中阶段知识体系的安排导致学生对相关知识的掌握并不全面，然而学生却浑然不知。当在大学阶段再次学到相关知识时，学生误以为是简单重复，认为自己已经完全掌握了该知识，所以对大学老师的讲解不会给予足够的重视，这势必会导致学生所掌握的知识不具备系统性和完整性，并会影响到后续内容的学习。

（五） 初等数学与高等数学并非无缝衔接

随着高考的不断改革，初等数学在教学内容上也做出了相应的调整。从教材内容来看，目前的初等数学知识与高等数学知识本身是衔接的，而且还有部分重叠。但是由于学生来自不同的省份，而且有文理科之分，所以对数学的学习要求并不相同，这就导致并非所有出现在高中教材中的知识，学生在高中就一定学习或者掌握了，而且有的知识部分学生学过，部分学生又没有学。例如：极坐标的基础知识在高中属于选修内容，大部分理科生接触过相关知识，但文科生对该知识一般不作要求；三角函数的和差化积公式与积化和差公式属于必修内容，在高中数学教材人教B版必修四中有介绍，但这两套公式在高中并不要求学生记忆，只需掌握证明方法就可以，所以学生对相关公式的熟悉程度也是不尽相同。

虽然从理论上讲，考进同一所高校，特别是同一个专业的学生的学习水平应该是相当的，然而上述客观背景导致处在同一所高校、同一个专业这样一个相同起跑线上的学生的知识储备其实是参差不齐的。进入大学以后，相同的课程使用相同的教材，不会再区分地域以及文理科，因此需要大家有统一的基础，这就导致对于部分学生而言，从初等数学到高等数学并未实现无障碍衔接，他们缺乏学习高等数学必备的一些基础知识。

（六）教材内容与生活及专业关联度不高

数学起源于人类早期的生产活动，人们对客观世界首先进行定性把握，然后进行定量刻画，最后逐渐过渡到抽象概括，形成系统的理论与方法，便产生了数学。数学是人们生活、劳动和学习中必不可少的工具，生活中处处有数学，处处需要数学。作为一门具体的数学课程，高等数学虽然以理论性、抽象性极强而著称，但同时其应用性也很强。高等数学在计算机、电子科技、航天技术、生物医学等众多领域均有广泛应用。例如在计算机领域，计算机中许多地方都要用到数学模型，特别是算法复杂度分析与算法优劣性的评价，还有人工智能、机器学习、大数据等方面的数学建模，都需要一定的高等数学知识作为基本功底。另外，随着现代科技的发展和计算机的应用与普及，数学方法在医药学中的应用日益广泛和深人，医药学科逐步由传统的定性描述阶段向定性、定量分析相结合的新阶段发展，数学方法为医药科学研究的深人发展提供了强有力的工具。