融通“一致性”的创生课堂

“一致性”是《义务教育数学课程标准（2022年版）》提出的一个重要名词，体现了教学内容体系的结构化，因此“帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化数学知识体系”成为创生课堂教学的核心目标。那如何在“一致性”的视角下创设创生课堂，把“一致性”贯穿于义务教育不同的学段呢？以小学数学教学实践为例，我有如下思考。

片段一：融通分数、小数、整数基于计数单位表达的一致性

（一）自主选择，多元表征一位小数的意义

1.出示探究活动一：探究一位小数0.6表示的意义。

2.学生动手操作并尝试交流。

3.学生展示作品并说出自己的想法。

4.问题引领，自主思考。问题1：选择不同的图形，表示出的却都是0.6，为什么？

生：不管选什么图形，都是把它平均分成10份，每份是 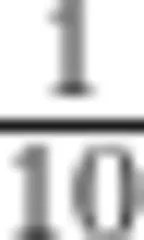，也就是0.1，数出其中的6份， 6 份是6个0.1，6个0.1是0.6，0.6等于10。

问题2：一位小数表达的意义是什么？

生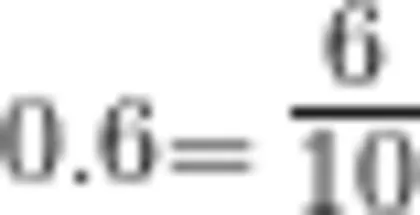： ，零点几就等于十分之几，一位小数的意义就是可以化为分母是10的分数。

小结：上面这些图形存在的意义首先是一个度量单位，当度量的对象用整数1不够表达时，需要把单位细分，产生更小的度量单位。它们不仅可以表示1元、1米、1公顷、1个物体，还可以表示许多个物体组成的一个整体，如果不带单位，它们就是单位“1”，由此说明度量单位和单位“1”是一致的。单位“1”选用什么图形来表示不重要，重要的是要把单位“1”平均分成10份，每份是 也就是0.1，数出其中的6份，6个0.1累加就是 0.6 （204

（二）类比迁移，沟通一致性

师：我们探究了一位小数的意义，接下来把一位小数0.1平均分成10份，每份就是0.01，0.01也就是 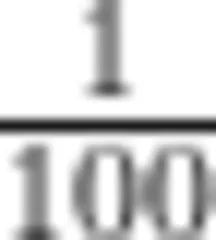如此依次往后细细十等分，就能探究多位小数的意义。

动画演示数线图图1，你发现了什么？

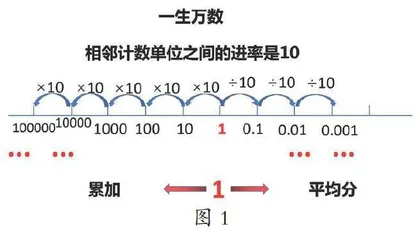
生：把整数部分最小的计数单位“1”均分10份，每份是 0.1， 0.1 就是 10；0.1再均分10份，每份是0.01，0.01也就是 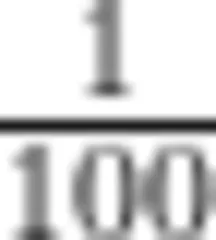； ；0.01再均分10份，每份是0.001，0.001也就是 。

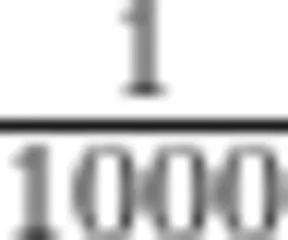师：这条平均分的路，有尽头吗？生：没有尽头，可以无限分下去。师：从0.001往左看，你发现了什么？众生：10个0.001累加是0.01，10个0.01累加是0.1，10个0.1累加是1，10个1累加是10。

师：这条累加的路有尽头吗？生：没有尽头，可以无限累加上去。

小结：从计数单位“1”开始，向右不停地细细均分，所分得的计数单位越来越小，这些很小很小的计数单位可以组成很多很多的小数，进而转化为分数；如果向左不停地累加，所得的计数单位越来越大，这些很大的计数单位可以组成很多很多整数，整数和小数组合起来，又是无穷无尽的小数，夸张地说，“1”生万数。

（三）回归计数器，再次融通一致性

师：观察图2，你发现了什么？

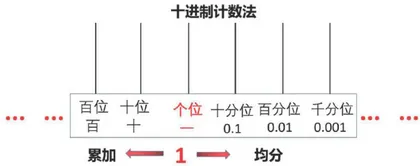
生1：从计数单位“1”开始，向左是不停地累加，向右是不停地平均分。

生2：计数器表示的是十进制计数法，和我们今天学的是一致的，每相邻的两个计数单位之间的进率都是10。

思考：小数本质上是十进分数的另一种表达形式，我们在进行度量或计算时，很多时候不能得到整数的结果，这时就常用小数来表示，小数能更加精准地表达数据。本片段就是按照“向左是依次满十进一，向右是依次十等细分”的规则，打通了整数、分数、小数之间的关联和一致性，从而构造了完整的位值计数系统。

片段二：融通乘法运算基于计数单位表达的一致性

（一）探究三位数乘两位数的笔算

问题情境：今年的九九重阳节，安康社区为区内每个老人献一束鲜花，每束鲜花都搭配2朵玫瑰和10朵康乃馨，寓意祝福老人一年十二个月幸福安康。李阿姨要配齐145束鲜花，一共需要多少朵？

师：怎么列式解决？

生： 2+10=12 （朵）， 145×12= 。

师：如何笔算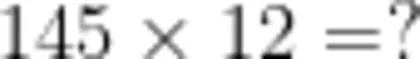

1.出示探究活动一。

活动要求：

（1）算一算：在练习单上尝试列竖式计算；

（2）说一说：小组内说一说，你是怎样计算的；

（3）验一验：在练习单上验证，计算结果正确吗？

2.学生尝试计算并在小组内交流。

3.学生展示作品并说出自己的计算过程。

4.问题引领，自主思考

问题1：上图竖式中的数字290表示什么？

生：表示为145位老人准备的玫瑰花是145朵。

问题2：数字145末尾为什么要对齐十位？

生1：145是十位上的1去乘145的得数，表示145个十，所以数字“5”对齐十位。

生2（补充）：最后实际是 290+1450 ，也就是把前面两次乘得的290个一、145个十累加，得数是 1740 。（204号

问题3：怎样判断计算结果是否正确呢？

生1：可以估算， 145≈150，12≈10 ，150×10=1500 ，与1740比较接近。

生2：可以交换两个因数的位置，用 12×145 来验算。

（二）类比迁移，融通乘法算理的一致性

1.出示探究活动二。

活动要求：

（1）算一算：笔算 1234×123

（2）比一比：对比 145×12 的算法，你发现了什么？

2.学生动手操作并尝试交流。

3.学生交流反馈。

生1：对比算法，它们的算法是一致的。

生2：它们的算理也是相通的。

4.融通一致性。

师：三位数乘两位数，怎么计算？众生齐说，动画依次同频出示图3第一个竖式。

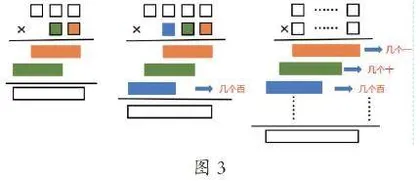
师：四位数乘三位数，又怎么计算？众生齐说，动画依次同频出示图3第二个竖式。

师：多位数乘多位数呢？

众生齐说，动画依次同频出示图3第三个竖式。

思考：无论是整数乘法中的多位数乘多位数，还是以后要学的小数乘小数，都是先用第二个因数右边数起的第一位、第二位、第三位分别去乘第一个因数，得到第一层、第二层、第三层最后把每一层得到的若干个计数单位累加，累加的得数就是运算的结果。

片段三：融通“路程模型”基于结构的一致性

（一）问题引领

核心问题：以行程问题基本模型“路程=速度 × 时间”为核心，在流水行船中如何通过变式与拓展，形成模型大结构？

（二）融通一致性

1.设置问题链，探究流水行船中的“船速”。

问题1：什么是“船速”？

生：船在静水（不会流动的水）中航行的速度。

情境：2024年巴黎奥运会中，中国选手刘浩/季博文在静水男子500米双人划艇比赛中以1分39秒48的成绩获得冠军，该赛艇的“船速”是多少？

问题2：求船速，对应的数量关系式是？

生：速度=路程 ÷ 时间。

2.设置问题链，探究流水行船中的路程。

问题1：轮船顺流而下时，实际路程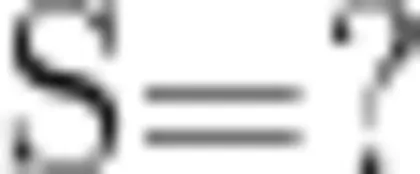

情境：2024年10月11日至13日，2024年国际皮划艇联合会“杭州超级杯”在杭州富阳举行，刘浩、季博文等13位世界奥运冠军参赛。比赛结束之后，刘浩和其他运动员乘坐富春山居号游船以50千米／时的“船速”顺流而下，游玩了2小时，江水流速为1.5千米／时，他们在水上航行了多远？

问题2：求路程，对应的数量关系式是？实际速度 v 怎么计算？

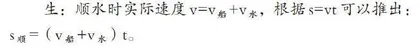
问题3：解答正确吗？

问题4：返回时轮船逆流而上，如果“船速”不变，实际路程 S=Ω ？

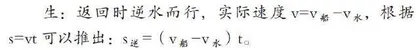
3.设置问题链，探究流水行船中的时间。