在数学教学中让学生感悟“数学思想

在小学数学教学中，不仅要注重基础知识，更要注重数学思想与方法的渗透。这就要求教师认真解读教材，挖掘数学知识中隐含的“数学思想”，引导学生领悟数学思想，提高学生应用“数学思想”的意识，去解决日常生活中的实际问题。

一、在情境中，感悟“分类”思想

分类的过程就是对事物共性的抽象过程。教学时，教师应让学生不断地感受到分类的重要性，并懂得怎样进行分类，明确分类的标准，对不同性质东西进行有效区分，让学生不断地意识到分类是一种非常重要的思想与方法。学会了分类，有助于学生对所学新知进行分析与解决。

如，在教学“分类与整理”一课时，教师先创设了“分气球”的问题情境，并通过三层分析来引导学生进行分类。

1.问：为什么要分类？因为要回答小精灵聪聪的问题“我想知道每种气球各有多少个，该怎么办？”。为此，我们要进行分类。

2.疑：如何分类？引导学生思考并质疑：“这么多的气球，大家可以怎样将它们进行分类呢？”

3.定：让学生懂得分类的方法，不同的区分方法得出的分类方式也是不一样的。引导学生可以按颜色或形状等不同的情况进行分类。

然后让同桌合作开展探究活动，活动要求：以同桌合作开展活动，从信封中取出一些气球卡片，先确定分类标准，再进行分类，思考还有其他分类办法吗？

这样，让学生自己选择分类的方式进行解决，从而感悟到由于标准不同分类结果也不一样，体验分类的多样性，不仅有利于学生对分类活动的认识，而且加深对分类的理解。

二、在比较中，感悟“对应”思想

“对应思想”是指在两类事物（集合）之间建立某种联系的思维方法。在小学数学教学中，对应思想在数学课堂上经常用到，把“一一对应”作为一种数学思想方法渗透于学生数学学习的过程之中，充分地创设认知冲突的问题情境。并在数与数、数与形、形与形、量与量等变化规律中，不仅考虑显性的知识，更要充分挖掘其中大量的对应关系。

如，在教学“植树问题”一课时，师出示如下信息：20棵树排成一行，每相邻的两棵树之间摆一盆花，头尾都不放花，一共摆了多少盆花？这样的问题，许多学生容易出错，针对这种情况，教师就可以利用“对应思想”帮助学生理清思路：从头开始，一棵树对应一盆花，一一对应后，最后的一棵树很孤单，没有花盆与它对应，所以“间隔数”比“树的棵数”少1，一共可以放19盆花。又如，还是这20棵树，每相邻的两棵树之间放一盆花，头尾都放，一共可放多少盆花呢？此时，通过刚才“对应思想”的渗透，很多学生已经能够自己借助图示用“一一对应”的方法解释：“间隔数”比“树的棵数”多1，所以，花的盆数是 20+1=21 （盆）。

三、在计算中，感悟数形结合思想

在小学数学的计算教学中，小学生往往因为计算方法混淆，导致计算错误。原因是对算理不能理解，计算只停留于机械记忆。那么，如何帮助学生理解算理既是计算教学的重点，又是难点。为此，教师通常借助课件的演示或直观学具的演示，引导学生在动手操作与观察思考中去理解算理，从而使计算的算理可视化。

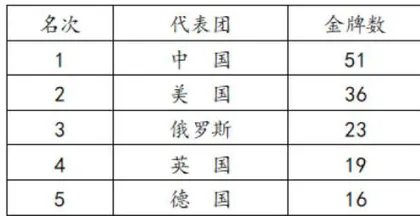
如，在教学“100以内进位加法”一课时，出示（图1）从图中得到的数学信息，先让学生说一说，再让学生说依据数学信息，可提出什么数学问题。生1：美国的金牌拿得比俄罗斯多多少？学生根据问题寻找解决问题所需要的条件，并尝试进行计算。学生很快进行计算；然后在小组内交流自己的算法。最后指名汇报、交流算法，师生评价。在汇报算法时，学生更是各抒己见：

生1： 6-3=3 ，30-20=10，3+10=13，所以36-23=13。

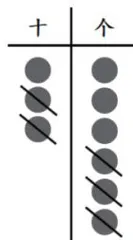
生2：有学生在计数器十位上拨3颗珠子，个位上拨6颗珠子，表示36；然后减去23就在个位上去掉3颗珠子，在十位去掉2颗珠子，只剩下十位1颗珠子，个位3颗珠子，也就是13。

生3：有的学生直接用竖式进行计算。

…..

计算中，学生主动应用数形结合的思想学习新知识、理解算理、掌握算法，为后续学习多位数加减法计算打下基础。

2008年北京奥运会金牌榜前5名如下表：

生2：美国与英国一共得了多少块金牌？列式为：36+19=。

让学生利用原有的学习经验进行计算，发现个位相加满十，应该怎么办？此时，教师不要急于教给方法，让学生利用小棒动手摆一摆，摆的时候满10根捆成一捆。师问：现在零散的小棒有几根？又有几捆小棒呢？有了直观的动手操作之后，并在教师的追问下，学生将感性活动认知慢慢转化为理性的认知，从而突破了难点，也渗透了数形结合思想。

因此，在计算过程中，借助动手操作，帮助学生进行计算，同时学生能够在数形结合中很好地理解算理。

四、在训练中，体验“化归”思想

在小学数学教学中，应加强新旧知识的联系，帮助学生从感性的认识上升到理性的思考，把抽象的知识形象化，通过转化，归结为一般的数学方法和解题策略，有利于学生对知识的建模。

如，在教学“正比例和反比例”一课时，师创设学校运动会上的“60米赛跑”情境，引导学生进行分析比较，来理解“正比例、反比例”的意义。在路程一定的情况下，若甲与乙的速度比是 3：2 ，那么甲和乙所行的时间比就是 2：3 ，学生在亲历的情境中更好地理解“路程一定，速度和时间成反比例”；接着继续以甲、乙两人为例，两人同时同地出发跑了15秒，也就是时间一定的情况下，如果他们的速度比是 3：2 ，则所行的路程比也是 3：20 学生更容易地理解“时间一定，路程和速度成正比例”。

这样，把抽象的正比例和反比例知识同生活紧密联系起来，进行巧妙地转化，使知识的学习不仅仅局限于“积一定，成反比例；商一定，成正比例”的抽象文字记忆中，而是在学生的头脑中形成更加直观的表象，形成鲜明的知识体系，更有利于学生建立完善的正比例和反比例的概念。为此，让学生用化归思想方法去思考问题，去探究新知，有效培养学生探究新知的能力，从而深度地理解所学知识的内涵。

五、在变化中，感悟“转化”思想

“转化”思想是研究和解决相关数学问题时常用到的数学思想方法，它将一种形式转变成另一种形式，可以变新知为旧知、变复杂为简单、变抽象为形象，从而帮助学生解决有关的问题，感悟转化思想的价值。

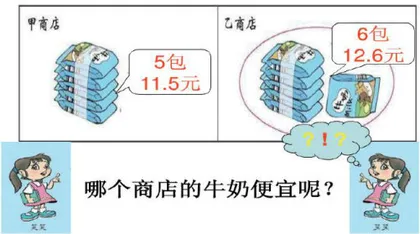
如，在教学“除数是一位数的小数除法”一课时，教师创设“超市购物付钱”的问题情境：

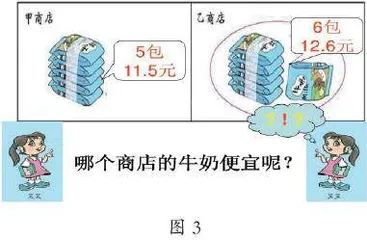
先让学生独立思考、自主探究，进行尝试解决，然后指名汇报：

通过交流互动，明白学生的想法：把小数先转化为整数计算，将已有的学习经验迁移到新知学习之中，引发学生去思考、去尝试、去探究、去解决，逐步进行延伸，如图6，通过转化找到问题本质，从而学会新知。

总之，数学思想的有机渗透，需要经历一个过程。教学中，教师应关注学生的学习过程，训练学生的思考过程，让学生在数学学习中体会数学思想的价值，为学生的可持续发展奠定基础。